Thread by 10-K Diver
- Tweet
- Jan 1, 2023
- #DecisionMaking #Probability #GameTheory
Thread
1/
Get a cup of coffee.
In this thread, I'll walk you through "Gambler's Ruin".
This is a classic exercise in probability theory.
But going beyond the math, this exercise can teach us a lot about life, business, and investing.
Get a cup of coffee.
In this thread, I'll walk you through "Gambler's Ruin".
This is a classic exercise in probability theory.
But going beyond the math, this exercise can teach us a lot about life, business, and investing.
2/
In my mind, Gambler's Ruin is the math of "David vs Goliath" ("Skill vs Size") type situations.
Here, David is a "small" player. He only has limited resources. But he's very skilled.
Pitted against David is Goliath -- a "big" player who has MORE resources but LESS skill.
In my mind, Gambler's Ruin is the math of "David vs Goliath" ("Skill vs Size") type situations.
Here, David is a "small" player. He only has limited resources. But he's very skilled.
Pitted against David is Goliath -- a "big" player who has MORE resources but LESS skill.
3/
The battle between David and Goliath rages on for several "rounds".
Each round has a "winner" -- either David or Goliath.
David -- because of his superior skill -- has a higher probability of winning any individual round. That's David's advantage over Goliath.
The battle between David and Goliath rages on for several "rounds".
Each round has a "winner" -- either David or Goliath.
David -- because of his superior skill -- has a higher probability of winning any individual round. That's David's advantage over Goliath.
4/
But because of the size asymmetry between the players, the loss of a round *impacts* David more negatively than Goliath.
In other words: Because Goliath starts out with more resources, he's able to take more punches than David.
That's Goliath's advantage.
But because of the size asymmetry between the players, the loss of a round *impacts* David more negatively than Goliath.
In other words: Because Goliath starts out with more resources, he's able to take more punches than David.
That's Goliath's advantage.
5/
The way this works is:
After each round, the *loser* gives the *winner* some of their resources.
This goes on until one of the players is wiped out -- ie, has no more resources left.
The way this works is:
After each round, the *loser* gives the *winner* some of their resources.
This goes on until one of the players is wiped out -- ie, has no more resources left.
6/
Let's take an example.
Suppose David brings $2000 to the table. And Goliath brings $10000.
Thus, at the start of the game, Goliath's bankroll is 5x David's.
This is Goliath's "size" advantage.
Let's take an example.
Suppose David brings $2000 to the table. And Goliath brings $10000.
Thus, at the start of the game, Goliath's bankroll is 5x David's.
This is Goliath's "size" advantage.
7/
But offsetting this, David has a "skill" advantage.
Let's say this gives David a 55% chance of winning any given round -- as opposed to Goliath's 45%.
But offsetting this, David has a "skill" advantage.
Let's say this gives David a 55% chance of winning any given round -- as opposed to Goliath's 45%.
8/
And we'll say each round costs the loser $1000, which gets added to the winner's bankroll.
With these rules, we can see that Goliath only needs to win *2* rounds more than David.
That's enough to wipe out David's $2000 -- bankrupting him and costing him the battle.
And we'll say each round costs the loser $1000, which gets added to the winner's bankroll.
With these rules, we can see that Goliath only needs to win *2* rounds more than David.
That's enough to wipe out David's $2000 -- bankrupting him and costing him the battle.
9/
But for David to come out on top, he has to win *10* rounds more than Goliath.
Only then will David be able to take away Goliath's $10000 and bankrupt him.
Seems like a tall order. But we must remember: each *individual* round favors David 55 to 45.
But for David to come out on top, he has to win *10* rounds more than Goliath.
Only then will David be able to take away Goliath's $10000 and bankrupt him.
Seems like a tall order. But we must remember: each *individual* round favors David 55 to 45.
10/
So, who is more likely to win this battle: David or Goliath?
Is David's 55/45 "skill" advantage enough to overcome Goliath's $10K/$2K "size" advantage?
More generally, how much skill does an underdog need to offset an incumbent's size?
That's the Gambler's Ruin puzzle.
So, who is more likely to win this battle: David or Goliath?
Is David's 55/45 "skill" advantage enough to overcome Goliath's $10K/$2K "size" advantage?
More generally, how much skill does an underdog need to offset an incumbent's size?
That's the Gambler's Ruin puzzle.
11/
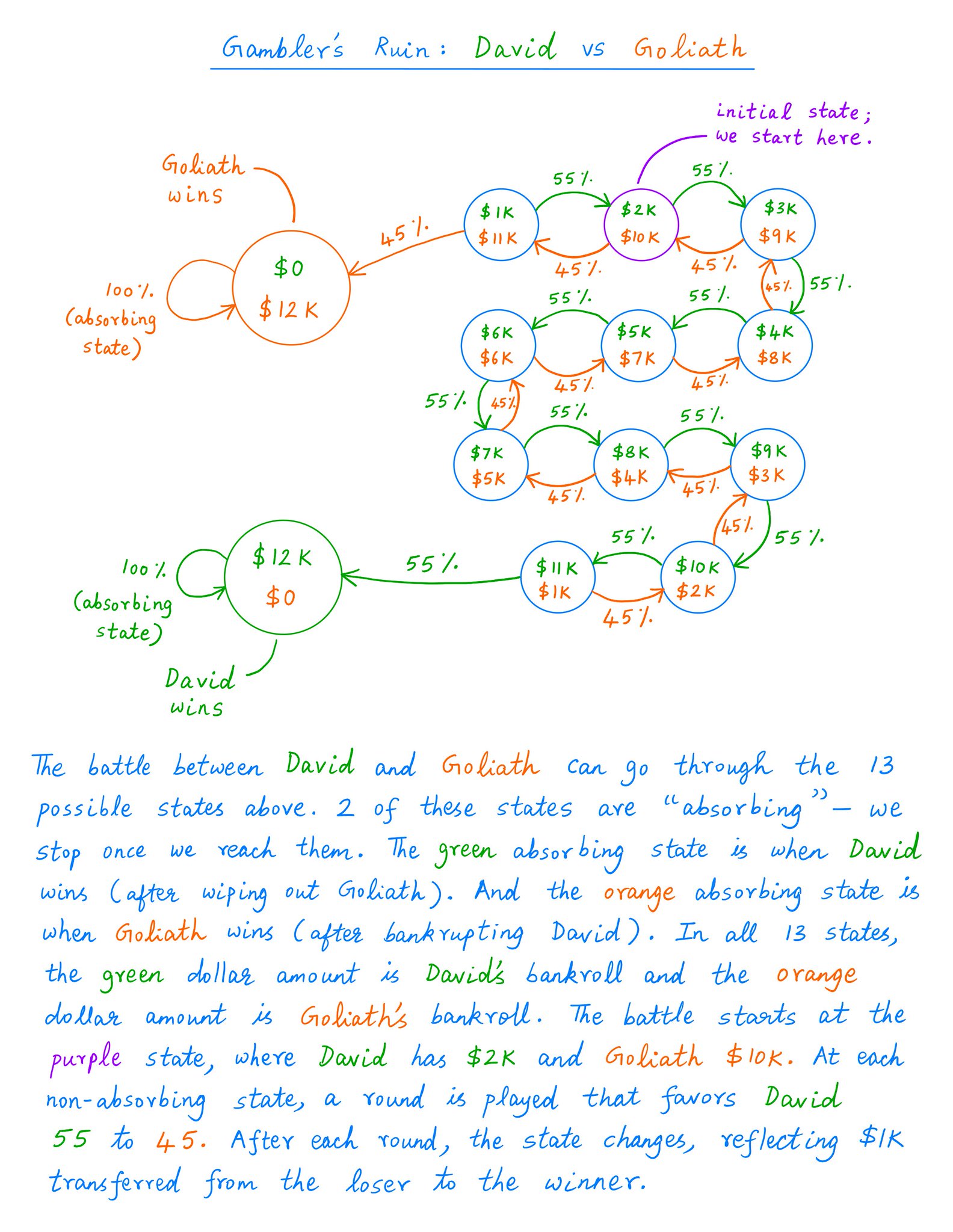
Here's a picture showing all possible states that David and Goliath can go through -- before one of them eventually vanquishes the other.
Here's a picture showing all possible states that David and Goliath can go through -- before one of them eventually vanquishes the other.
12/
Mathematicians have a special name for this kind of state-based picture. They call it a Markov Chain.
Markov Chains are a standard topic covered in introductory probability courses.
To learn more about them, please see:
Mathematicians have a special name for this kind of state-based picture. They call it a Markov Chain.
Markov Chains are a standard topic covered in introductory probability courses.
To learn more about them, please see:
13/
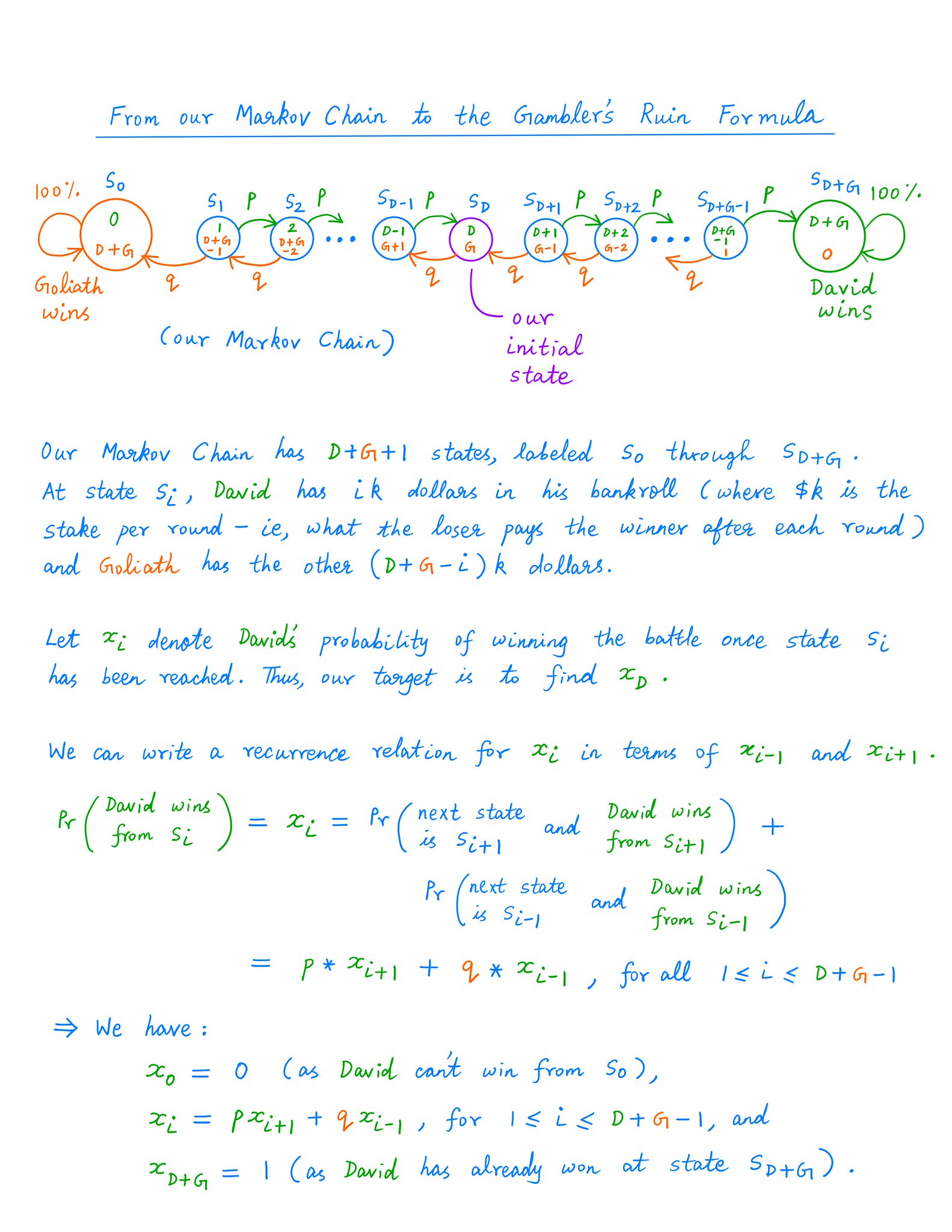
There are many clever ways to analyze Markov Chains.
And one such way lets us solve our Gambler's Ruin puzzle.
This gives us a formula to calculate David's and Goliath's respective probabilities of winning the battle:
There are many clever ways to analyze Markov Chains.
And one such way lets us solve our Gambler's Ruin puzzle.
This gives us a formula to calculate David's and Goliath's respective probabilities of winning the battle:
14/
Applying this formula, we see that David only has a ~36% chance of winning our battle -- ie, the odds favor Goliath nearly 2 to 1.
Thus, David's 55/45 "skill" advantage is NOT enough to overcome Goliath's $10K/$2K "size" advantage when the stakes are $1000/round.
Applying this formula, we see that David only has a ~36% chance of winning our battle -- ie, the odds favor Goliath nearly 2 to 1.
Thus, David's 55/45 "skill" advantage is NOT enough to overcome Goliath's $10K/$2K "size" advantage when the stakes are $1000/round.
15/
For those who want to see how this Gambler's Ruin formula arises from the Markov Chain above, here's the math.
(Please don't worry if you don't get this math. I promise you won't need it for the rest of this thread!)
For those who want to see how this Gambler's Ruin formula arises from the Markov Chain above, here's the math.
(Please don't worry if you don't get this math. I promise you won't need it for the rest of this thread!)
16/
To me, Gambler's Ruin is more than a simple mathematical exercise.
I think it can teach us at least 5 key lessons relevant to life, business, and investing.
👇👇👇
To me, Gambler's Ruin is more than a simple mathematical exercise.
I think it can teach us at least 5 key lessons relevant to life, business, and investing.
👇👇👇
17/
Key Lesson 1: Life is probabilistic. So, we should think probabilistically -- not deterministically.
For example, suppose David's skill gives him an 80/20 advantage over Goliath.
In this case, David nearly always overcomes Goliath's size advantage (~94% of the time):
Key Lesson 1: Life is probabilistic. So, we should think probabilistically -- not deterministically.
For example, suppose David's skill gives him an 80/20 advantage over Goliath.
In this case, David nearly always overcomes Goliath's size advantage (~94% of the time):
18/
But even a 94% chance of victory is NOT a slam dunk. There's still a slim chance of Goliath beating David.
So, if we're betting on David to win, we should take these odds into account.
For example, we shouldn't put ALL our money behind David. That would be risking ruin.
But even a 94% chance of victory is NOT a slam dunk. There's still a slim chance of Goliath beating David.
So, if we're betting on David to win, we should take these odds into account.
For example, we shouldn't put ALL our money behind David. That would be risking ruin.
19/
Key Lesson 2: When we're up against someone who has far greater resources than us, we should strive to put the odds in our favor.
If the odds are just 50/50, and our opponent has infinitely deep pockets, we're *certain* to lose the battle.
Key Lesson 2: When we're up against someone who has far greater resources than us, we should strive to put the odds in our favor.
If the odds are just 50/50, and our opponent has infinitely deep pockets, we're *certain* to lose the battle.
20/
In fact, this is the origin behind the phrase "Gambler's Ruin".
If a gambler with limited resources and no edge keeps playing against a casino with practically infinite resources, the gambler will sooner or later be ruined.
In such situations, the house *always* wins.
In fact, this is the origin behind the phrase "Gambler's Ruin".
If a gambler with limited resources and no edge keeps playing against a casino with practically infinite resources, the gambler will sooner or later be ruined.
In such situations, the house *always* wins.
21/
Key Lesson 3: Low cost experiments tend to improve the odds of victory.
For example, when the stakes are $1000/round, we saw that Goliath's $10K/$2K size advantage gave him nearly 2 to 1 odds of victory, despite David's 55/45 skill advantage.
Key Lesson 3: Low cost experiments tend to improve the odds of victory.
For example, when the stakes are $1000/round, we saw that Goliath's $10K/$2K size advantage gave him nearly 2 to 1 odds of victory, despite David's 55/45 skill advantage.
22/
But what if we REDUCE the stakes to $100/round instead of $1000/round -- keeping everything else the same?
Now, the odds flip -- to *overwhelmingly* favor David. He ends up beating Goliath about 98% of the time!
But what if we REDUCE the stakes to $100/round instead of $1000/round -- keeping everything else the same?
Now, the odds flip -- to *overwhelmingly* favor David. He ends up beating Goliath about 98% of the time!
23/
Goliath still has the SAME $10K/$2K size advantage.
And David's skill advantage hasn't improved either. It's still 55/45.
So, how did David's probability of victory suddenly shoot up from ~36% to ~98%?
That's the power of each round being a "low cost" experiment.
Goliath still has the SAME $10K/$2K size advantage.
And David's skill advantage hasn't improved either. It's still 55/45.
So, how did David's probability of victory suddenly shoot up from ~36% to ~98%?
That's the power of each round being a "low cost" experiment.
24/
You see, when each round costed $1000, all it took was *2* unlucky rounds to wipe out David. Even with 55/45 odds, that happens quite often.
But when each round costs just $100, it takes *at least 20* unlucky rounds to bankrupt David. At 55/45 odds, that's *very* unlikely.
You see, when each round costed $1000, all it took was *2* unlucky rounds to wipe out David. Even with 55/45 odds, that happens quite often.
But when each round costs just $100, it takes *at least 20* unlucky rounds to bankrupt David. At 55/45 odds, that's *very* unlikely.
25/
Folks like @JeffBezos intuitively understand the power of such low cost bets.
Even when an individual bet (like the Fire phone) fails, it's not likely to bankrupt the company. Underwriting many such low cost bets can be very profitable over time.
From Bezos's 2018 letter:
Folks like @JeffBezos intuitively understand the power of such low cost bets.
Even when an individual bet (like the Fire phone) fails, it's not likely to bankrupt the company. Underwriting many such low cost bets can be very profitable over time.
From Bezos's 2018 letter:
26/
Key Lesson 4: Prefer *non zero sum* games.
Gambler's Ruin is inherently zero sum. Every dollar lost by one player is gained by another. In this setting, one of the players will eventually be ruined.
Key Lesson 4: Prefer *non zero sum* games.
Gambler's Ruin is inherently zero sum. Every dollar lost by one player is gained by another. In this setting, one of the players will eventually be ruined.
27/
But what if each round were NOT zero sum? For example, what if the winner got $2 but the loser only lost $1?
In such "positive sum" cases, there's usually a good chance that both players survive indefinitely.
But what if each round were NOT zero sum? For example, what if the winner got $2 but the loser only lost $1?
In such "positive sum" cases, there's usually a good chance that both players survive indefinitely.
28/
That is, IF each round is sufficiently *positive sum*, even a weak player -- who is disadvantaged BOTH size-wise and skill-wise -- may end up with a high probability of surviving and thriving indefinitely.
So it may pay to seek out and play such infinite games.
That is, IF each round is sufficiently *positive sum*, even a weak player -- who is disadvantaged BOTH size-wise and skill-wise -- may end up with a high probability of surviving and thriving indefinitely.
So it may pay to seek out and play such infinite games.
29/
Key Lesson 5: If we're up against a powerful opponent, we should try hard to ensure they cannot use their FULL strength against us.
Gambler's Ruin is a classic example. It doesn't matter if Goliath has $1M. If each round just takes $1K, the other $999K simply sits idle.
Key Lesson 5: If we're up against a powerful opponent, we should try hard to ensure they cannot use their FULL strength against us.
Gambler's Ruin is a classic example. It doesn't matter if Goliath has $1M. If each round just takes $1K, the other $999K simply sits idle.
30/
David is much better off playing Goliath $1K at a time.
This type of disruption is all too common in business. Small upstarts often compete in a niche area that big players don't care too much about. From this foothold, the upstart expands to become a serious threat.
David is much better off playing Goliath $1K at a time.
This type of disruption is all too common in business. Small upstarts often compete in a niche area that big players don't care too much about. From this foothold, the upstart expands to become a serious threat.
31/
Here's a lovely article by James Allworth (@jamesallworth) explaining how this kind of dynamic played out between Arm and Intel:
jamesallworth.medium.com/intels-disruption-is-now-complete-d4fa771f0f2c
Here's a lovely article by James Allworth (@jamesallworth) explaining how this kind of dynamic played out between Arm and Intel:
jamesallworth.medium.com/intels-disruption-is-now-complete-d4fa771f0f2c
Mentions
See All
Brian Feroldi @BrianFeroldi
·
Jan 1, 2023
A+ thread Excellent job!