Thread by Luka Piskorec
- Tweet
- Mar 15, 2022
- #CreativeCoding #GenerativeArt
Thread
Second lecture in Algorithmic Design course at
@AaltoARTS deals with fundamentals of algorithmic design - mathematical building blocks for computation.
Session 2.1. - Fundamentals
www.youtube.com/watch?v=QkhbWt0GUNE&t=747s
#algorithmicdesign #generativeart #computationaldesign
@AaltoARTS deals with fundamentals of algorithmic design - mathematical building blocks for computation.
Session 2.1. - Fundamentals
www.youtube.com/watch?v=QkhbWt0GUNE&t=747s
#algorithmicdesign #generativeart #computationaldesign
@AaltoARTS "The purpose of computing is insight, not numbers." quote by Richard Hamming.
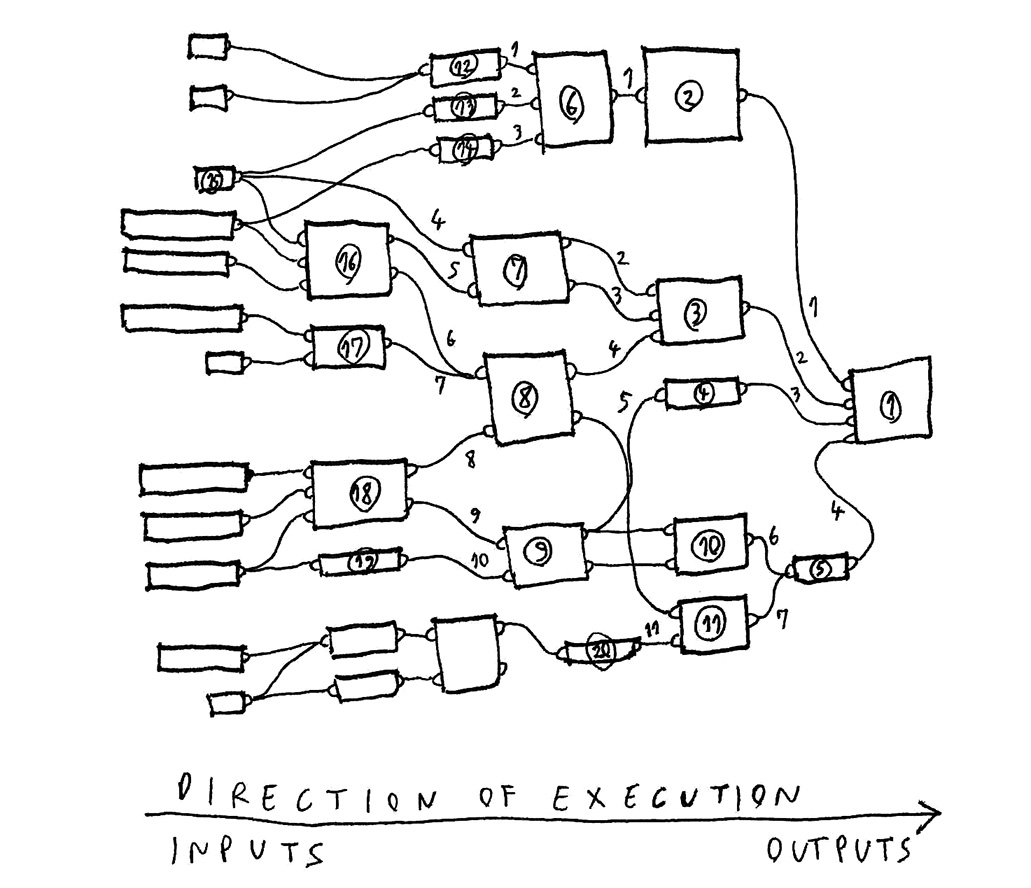
Computational design is about exposing the creative process by making it explicit, in form of a formal diagram or code. Designers are often not trained to do this, so they complain.
Computational design is about exposing the creative process by making it explicit, in form of a formal diagram or code. Designers are often not trained to do this, so they complain.
Reconstruction of Alberti’s map in “Descriptio urbis Romae”, by Luigi Vagnetti from 1974. Alberti described locations of monuments in Rome using polar coordinates, which is an early example of digital code representing spatial information.
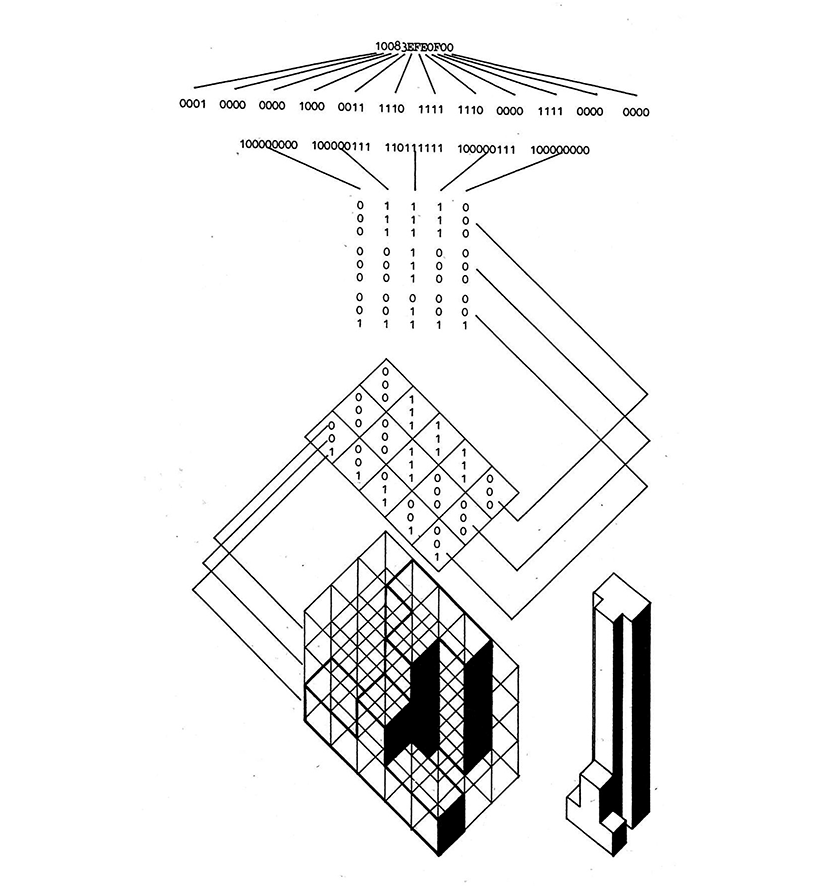
The hexadecimal code for Mies van der Rohe’s Seagram
building, by Lionel March, 1972. Today we would call this a "voxelized" representation.
#computationaldesign #voxels
building, by Lionel March, 1972. Today we would call this a "voxelized" representation.
#computationaldesign #voxels
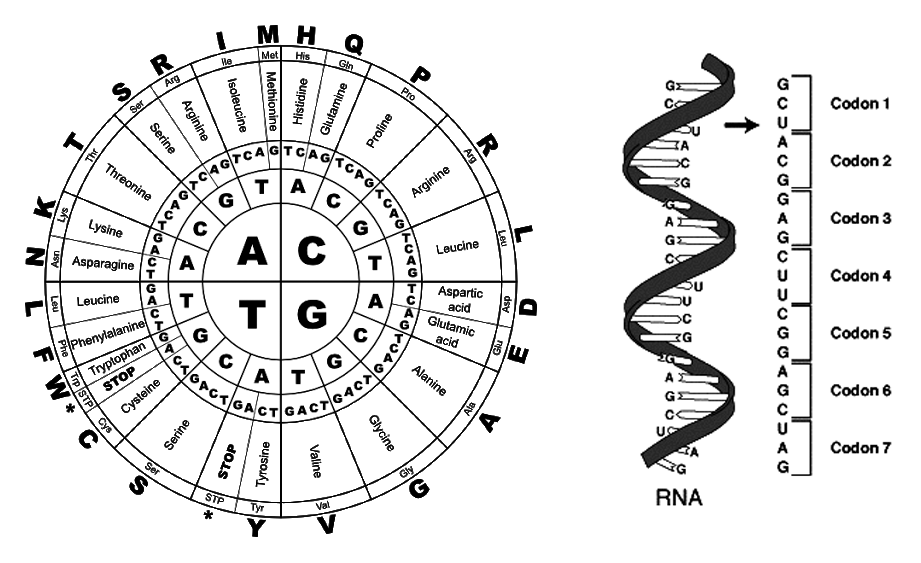
Code of Life
To decode a DNA codon, move from the center towards
the periphery (left). A series of codons in part of a messenger RNA molecule (right). This molecule will instruct a ribosome to synthesize a protein according to this code.
To decode a DNA codon, move from the center towards
the periphery (left). A series of codons in part of a messenger RNA molecule (right). This molecule will instruct a ribosome to synthesize a protein according to this code.
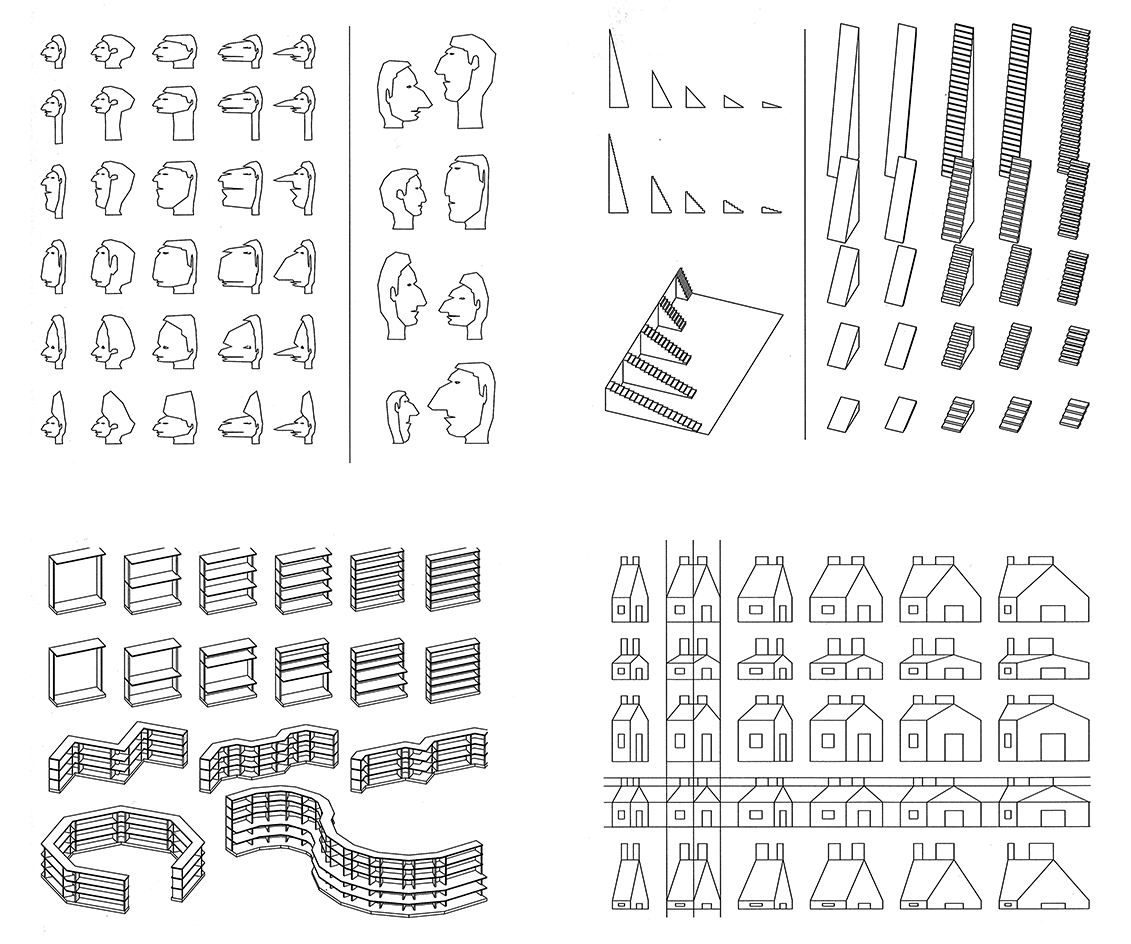
Design Space
In a parametric model, a dimension can be ascribed to every variable parameter, and thus the model becomes a many-dimensional space. Every point in that space represents a design solution. Diagrams below show solutions to different parametric models.
In a parametric model, a dimension can be ascribed to every variable parameter, and thus the model becomes a many-dimensional space. Every point in that space represents a design solution. Diagrams below show solutions to different parametric models.
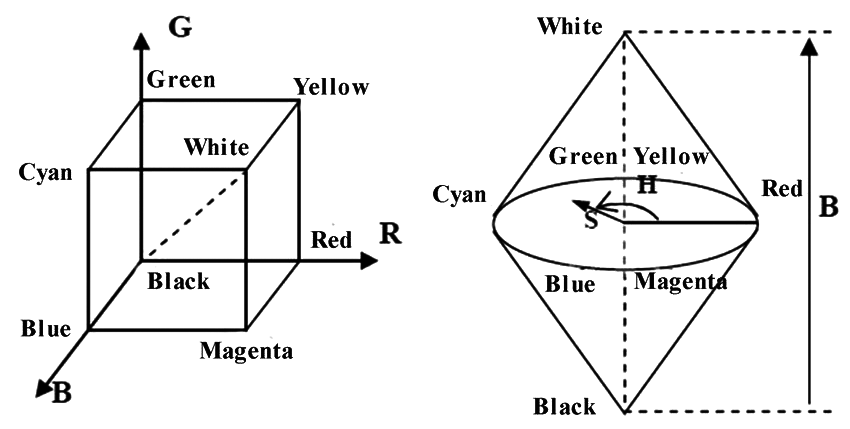
Color Space
RBG (left) and HSB (right) color spaces. RGB model is capturing physical principles behind mixing of light to create colors, but HSB is more intuitive and closer to how we think of colors. This insight came from @tylerxhobbs and his writings on color and code.
RBG (left) and HSB (right) color spaces. RGB model is capturing physical principles behind mixing of light to create colors, but HSB is more intuitive and closer to how we think of colors. This insight came from @tylerxhobbs and his writings on color and code.
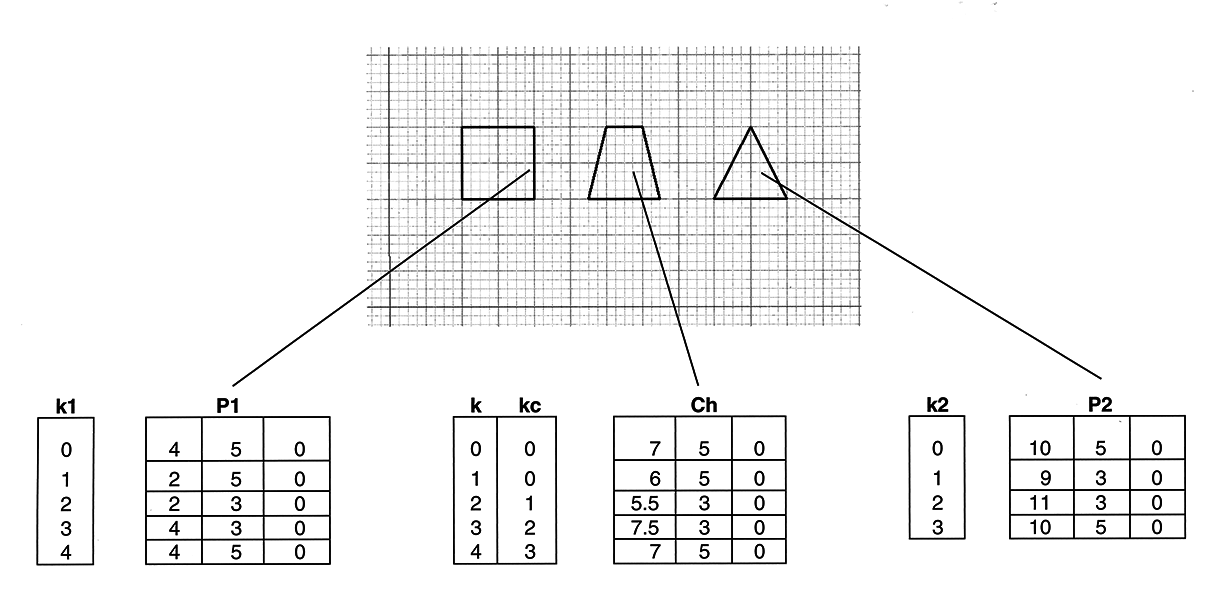
Vector Graphics
Polygons can be represented through a list of their vertices. The order of vertices encodes the edges of the polygon, which can be displayed by connecting adjacent vertices in the list.
Polygons can be represented through a list of their vertices. The order of vertices encodes the edges of the polygon, which can be displayed by connecting adjacent vertices in the list.
We can harness linear algebra to manipulate multi-dimensional arrays containing all kind of data inside, not just numbers. Below, examples of arithmetic operations on arrays in NumPy, a popular library for scientific computing.
#python #numpy
#python #numpy
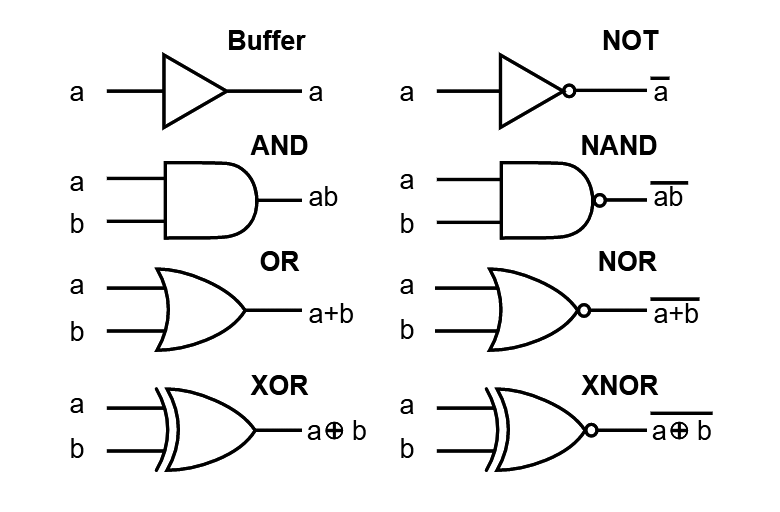
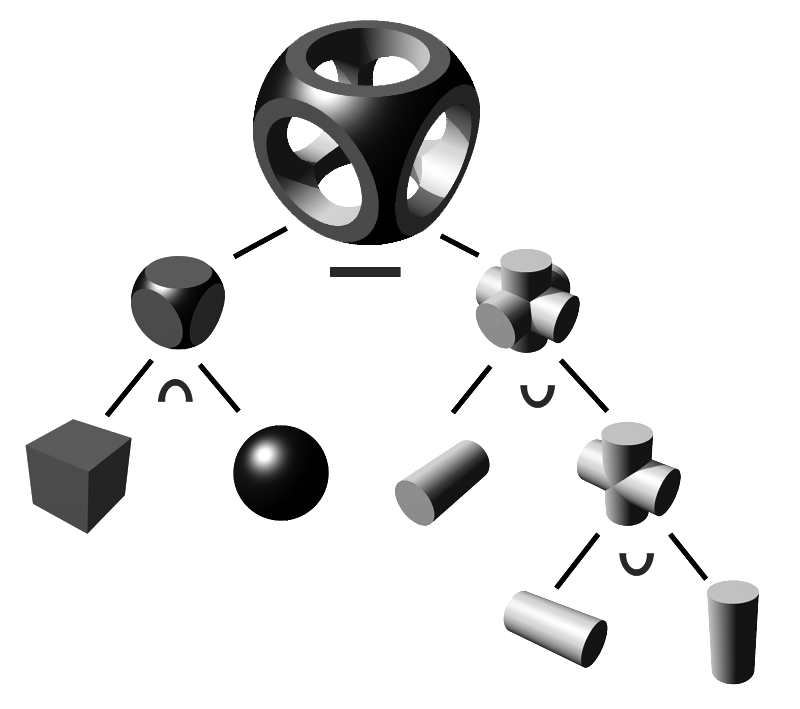
Boolean Algebra of Shapes
Boolean operations and digital logic gates (left) can be used for modeling 3D objects through CSG (constructive solid geometry) implemented in many CAD and modeling software. Foundation for this is set theory in mathematics.
#booleanalgebra #settheory
Boolean operations and digital logic gates (left) can be used for modeling 3D objects through CSG (constructive solid geometry) implemented in many CAD and modeling software. Foundation for this is set theory in mathematics.
#booleanalgebra #settheory
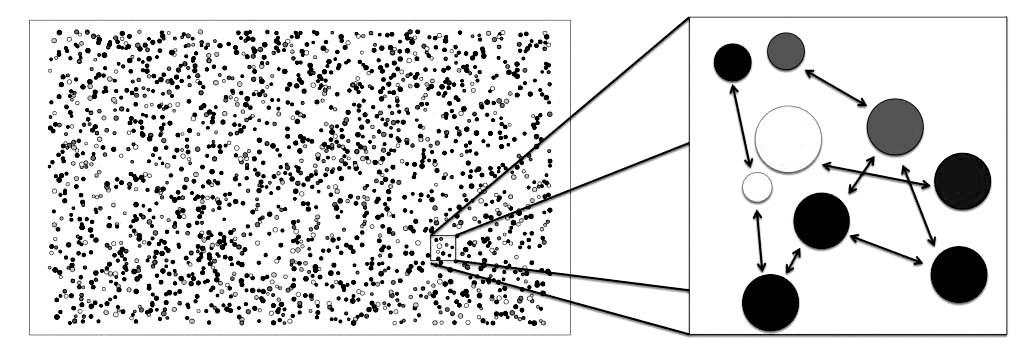
Concurrent models of computation - many similar parts acting locally in parallel
In algorithmic design, the most popular models of computation are concurrent models. Below, Game of Life cellular automata (left) and agent based model (right) are classic examples of these.
In algorithmic design, the most popular models of computation are concurrent models. Below, Game of Life cellular automata (left) and agent based model (right) are classic examples of these.
Four computer-generated random patterns based on the composition criteria of Mondrian’s “Composition With Lines”, by A. Michael Noll, 1965
#generativeart
#generativeart
In algorithmic design, randomness and its forms are essential for producing variation and introducing unpredictability. Diagram shows coverage of the unit square with randomly distributed points. Above for additive quasi-random numbers, below for pseudo-random numbers.
Pseudo-randomness in Nature
Rule 30 cellular automaton is a type of pseudo-random number generator. Interestingly, Conus textile shell pattern is similar in appearance to Rule 30 🤯
#rule30 #cellularautomata
Rule 30 cellular automaton is a type of pseudo-random number generator. Interestingly, Conus textile shell pattern is similar in appearance to Rule 30 🤯
#rule30 #cellularautomata
Recommended reading:
“The Logic of Architecture - Design, Computation and
Cognition” by William J. Mitchell (1986)
“Architecture After the Age of Printing” by Peter Eisenman (1992)
#algorithmicdesign #computationaldesign
“The Logic of Architecture - Design, Computation and
Cognition” by William J. Mitchell (1986)
“Architecture After the Age of Printing” by Peter Eisenman (1992)
#algorithmicdesign #computationaldesign