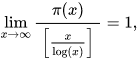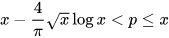Thread
1/n
Why are mathematicians interested in the distribution of prime numbers, and what do they actually mean by that?
A 🧵 on the Riemann hypothesis and Yitang Zhang's latest preprint on the Landau-Siegel zeros conjecture, which I covered yesterday
www.nature.com/articles/d41586-022-03689-2
Why are mathematicians interested in the distribution of prime numbers, and what do they actually mean by that?
A 🧵 on the Riemann hypothesis and Yitang Zhang's latest preprint on the Landau-Siegel zeros conjecture, which I covered yesterday
www.nature.com/articles/d41586-022-03689-2
2/
Questions on the statistics of prime numbers date back at least to one of the greatest mathematicians in history, the German Carl Friedrich Gauss, who in 1792 or 1793 (when he was at most 16 years old) noticed a pattern in their frequency
(Picture credit Mascdman/Wikimedia)
Questions on the statistics of prime numbers date back at least to one of the greatest mathematicians in history, the German Carl Friedrich Gauss, who in 1792 or 1793 (when he was at most 16 years old) noticed a pattern in their frequency
(Picture credit Mascdman/Wikimedia)
3/
It had long been known that larger and larger primes tend to space farther and farther apart from each other, but Gauss put a quantitative estimate on this using his prodigious mental abilities during an “idle quarter of an hour”, as he would later recall in his journal
It had long been known that larger and larger primes tend to space farther and farther apart from each other, but Gauss put a quantitative estimate on this using his prodigious mental abilities during an “idle quarter of an hour”, as he would later recall in his journal
4/
Gauss calculated that primes became rarer in proportion to their number of digits. This meant that to find an equal number of additional primes, one has to look at numbers (roughly) 10 times bigger
Gauss calculated that primes became rarer in proportion to their number of digits. This meant that to find an equal number of additional primes, one has to look at numbers (roughly) 10 times bigger
5/
The actual statement is about the asymptotic behavior of the function π(x), which counts how many prime numbers there are between 0 and x
The actual statement is about the asymptotic behavior of the function π(x), which counts how many prime numbers there are between 0 and x
6/
Gauss’s formula was soon independently rediscovered, but it took a while for it to be rigorously proved — by Jacques Hadamard and Charles Jean de la Vallée Poussin in 1896. It is now known as _the_ prime number theorem, par excellence
en.wikipedia.org/wiki/Prime_number_theorem
Gauss’s formula was soon independently rediscovered, but it took a while for it to be rigorously proved — by Jacques Hadamard and Charles Jean de la Vallée Poussin in 1896. It is now known as _the_ prime number theorem, par excellence
en.wikipedia.org/wiki/Prime_number_theorem
7/
But things that share a given asymptotic limit can still behave in wildly different and unpredictable ways. Just based on the prime number theorem, for example, there was no way of knowing if there would be larger and larger gaps containing no prime numbers at all
But things that share a given asymptotic limit can still behave in wildly different and unpredictable ways. Just based on the prime number theorem, for example, there was no way of knowing if there would be larger and larger gaps containing no prime numbers at all
8/
But in the meantime, Gauss’s star pupil Bernhard Riemann (my favorite mathematician of all time) took it one step further. In 1859 he offered a way to show that there would not be major statistical deviations from Gauss’s rule
But in the meantime, Gauss’s star pupil Bernhard Riemann (my favorite mathematician of all time) took it one step further. In 1859 he offered a way to show that there would not be major statistical deviations from Gauss’s rule
9/
To do so, he used a formula (now known as the Riemann zeta function) that had been invented a century before by Leonhard Euler, who also showed how it was intimately related to prime numbers
To do so, he used a formula (now known as the Riemann zeta function) that had been invented a century before by Leonhard Euler, who also showed how it was intimately related to prime numbers
10/
Riemann studied when the function yields zero, and where it doesn't — or shouldn't. He found that the absence of 'anomalous' zeros is equivalent to saying that the distribution of prime numbers isn't that wild after all
Riemann studied when the function yields zero, and where it doesn't — or shouldn't. He found that the absence of 'anomalous' zeros is equivalent to saying that the distribution of prime numbers isn't that wild after all
11/
Here's a beautiful example of what that would mean, found by Adrian Dudek in 2015: if the Riemann hypothesis is correct, then you can predict with certainty that there will be a prime number in any range of numbers of the form below
( see en.wikipedia.org/wiki/Riemann_hypothesis )
Here's a beautiful example of what that would mean, found by Adrian Dudek in 2015: if the Riemann hypothesis is correct, then you can predict with certainty that there will be a prime number in any range of numbers of the form below
( see en.wikipedia.org/wiki/Riemann_hypothesis )
The Riemann hypothesis has long been at the top of mathematicians' dreams. It was already included in the list of challenges for the new century that David Hilbert set out in the year 1900 at the International Congress of Mathematicians
en.wikipedia.org/wiki/Hilbert%27s_problems
en.wikipedia.org/wiki/Hilbert%27s_problems
13/
The Landau-Siegel zeros conjecture that Zhang has attacked has to do with another type of regularity in the distribution of primes, such as the fact that every arithmetic progression contains infinitely many primes, as was shown by Dirichlet in 1837
en.wikipedia.org/wiki/Dirichlet%27s_theorem_on_arithmetic_progressions
The Landau-Siegel zeros conjecture that Zhang has attacked has to do with another type of regularity in the distribution of primes, such as the fact that every arithmetic progression contains infinitely many primes, as was shown by Dirichlet in 1837
en.wikipedia.org/wiki/Dirichlet%27s_theorem_on_arithmetic_progressions
14/
This can be rephrased by saying that there are infinitely many primes that give a certain reminder when divided by another number
This can be rephrased by saying that there are infinitely many primes that give a certain reminder when divided by another number
15/
Again, saying that there are infinitely many is a statement about what happens at infinity, but the Landau-Siegel zeros conjecture guarantees that you don't have to wait a ridiculous amount of time to start seeing that pattern. Read my story for more!
www.nature.com/articles/d41586-022-03689-2
Again, saying that there are infinitely many is a statement about what happens at infinity, but the Landau-Siegel zeros conjecture guarantees that you don't have to wait a ridiculous amount of time to start seeing that pattern. Read my story for more!
www.nature.com/articles/d41586-022-03689-2
16/end
To conclude: many thanks to @AlexKontorovich and Andrew Granville for helping me orient myself on these abstruse questions
To conclude: many thanks to @AlexKontorovich and Andrew Granville for helping me orient myself on these abstruse questions
17/16 addendum:
At the end of the long thread I realized that I never actually answered my original question: Why are mathematicians interested in the distribution (i.e. the statistical properties) of prime numbers?
Uhm, why not!
At the end of the long thread I realized that I never actually answered my original question: Why are mathematicians interested in the distribution (i.e. the statistical properties) of prime numbers?
Uhm, why not!
18/16 addendum #2
Someone in my comments lamented that public funding for math is wasted. One should keep in mind that in the U.S., the NSF spends less than 3% of its $8 billion budget on math. The NIH budget is $45 billion and NASA's is another $24 billion
Someone in my comments lamented that public funding for math is wasted. One should keep in mind that in the U.S., the NSF spends less than 3% of its $8 billion budget on math. The NIH budget is $45 billion and NASA's is another $24 billion