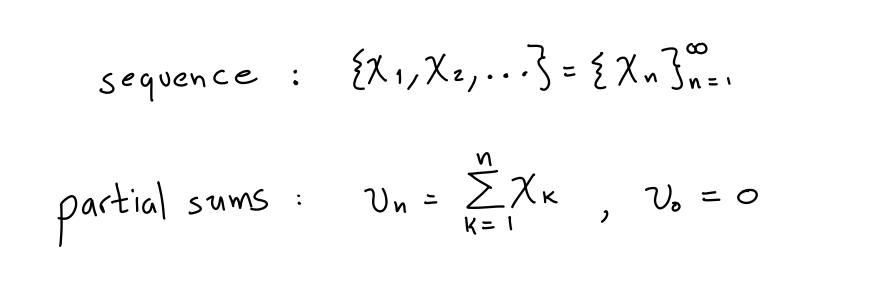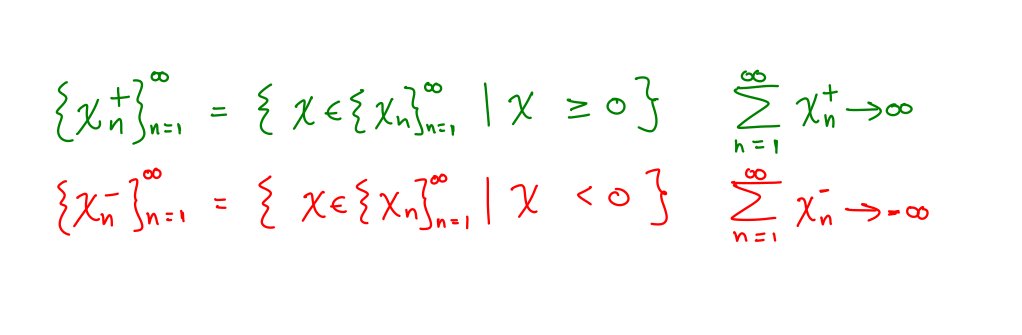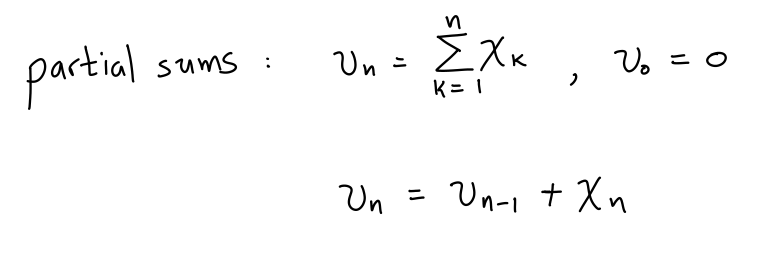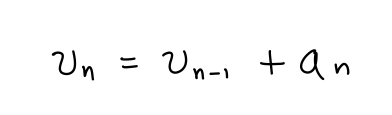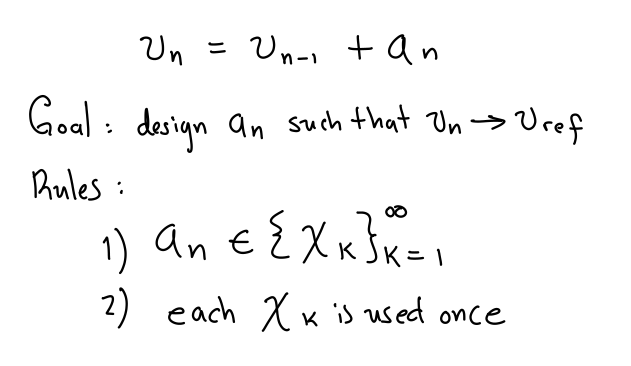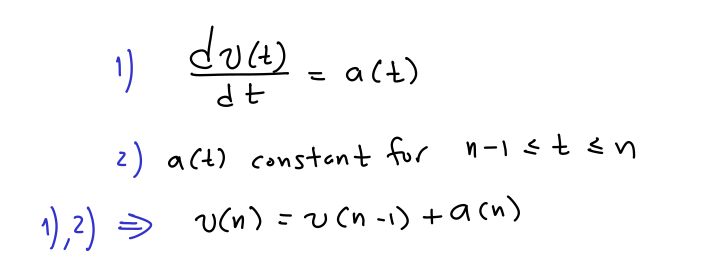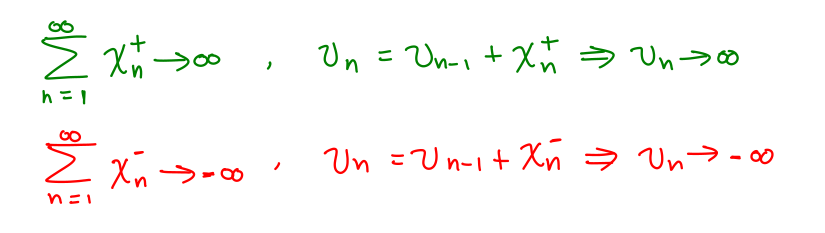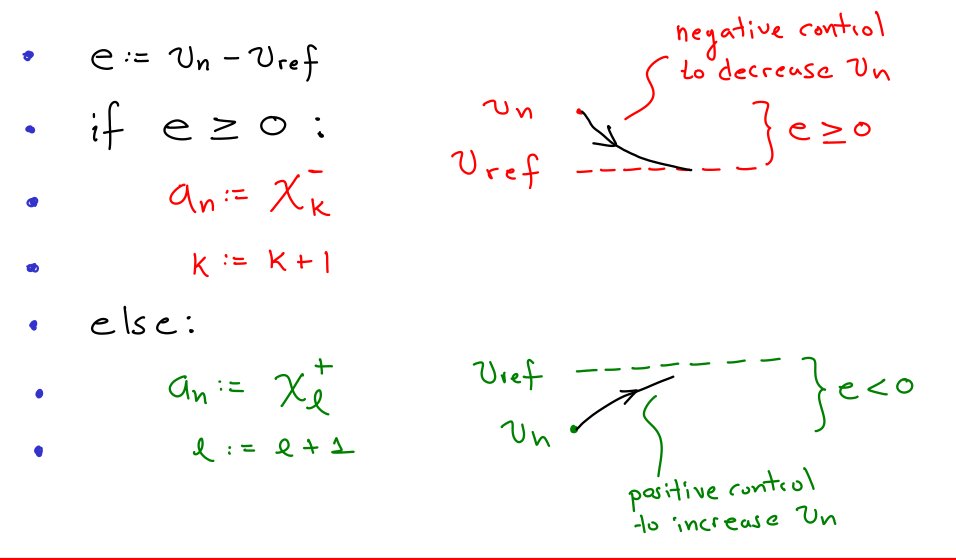Thread
1/ I saw this result in an analysis course many years ago. However, after four years of a control theory Ph.D., a very different interpretation came to my mind when rereading the proof. I'll explain the Riemann rearrangement theorem using control theory!
2/ First, I hope I don't do too many mistakes.
Now, the fundamentals of the problem: A conditionally convergent series is composed of a sequence of numbers ("x" in the image) whose partial sums "v" converge to some real number.
Now, the fundamentals of the problem: A conditionally convergent series is composed of a sequence of numbers ("x" in the image) whose partial sums "v" converge to some real number.
3/ However, if you split the numbers in the sequence into positive and negative ones and add them separately, these diverge.
4/ Now, partial sums for the sequence can be written recursively: partial sum at step "n" is the partial sum at step "n-1" just adding a new term x_n.
5/ By "rearranging" the original elements "x_n", we mean that instead of adding x_n in order, we add a term a_n which can be any element of the original sequence "x" as long as we do not repeat elements. This recursion is a "dynamical system" with state "v" and control "a."
6/ The control problem is to "design" the control a_n using only non-repeated elements from the original sequence to make the state (partial sums) converge to an arbitrary setpoint you want.
7/ To gain some intuition about this system, assume that "v" is the velocity of a car, and "a" is the acceleration.
8/ You can "control" the system by inducing a positive acceleration when pressing the gas pedal or inducing a negative acceleration by releasing it allowing friction of the road to slow down the car, or by pressing the brake directly.
9/ For example, the goal of cruise control is to measure the velocity and then apply (feedback) an appropriate acceleration to the car to reach and maintain a given velocity setpoint.
10/ The derivative of the velocity is acceleration. If we assume that the acceleration is maintained constant for each interval of unit length (1s or something smaller, you choose the units), the velocity evolves as in the original partial sum system
11/ This recursive equation is often called a "difference equation," "dynamical system," or simply "the system."
12/ Of course, in the cruise control example, the accelerations applied are not restricted to a sequence of numbers arising from a conditionally convergent series. However, this will help with intuition.
13/ The following is the most straightforward control idea to make the velocity reach a setpoint.
step 1) measure velocity and compute the error e = v - v_ref where v_ref is the velocity setpoint or reference we want to reach.
step 1) measure velocity and compute the error e = v - v_ref where v_ref is the velocity setpoint or reference we want to reach.
14/ step 2) if e >= 0, it means that v is above v_ref, then apply a negative acceleration to make v decrease
step 3) if e<0 it means that v is bellow v_ref. then apply positive acceleration to make v increase.
Most likely, this is what you do when driving (most of the time).
step 3) if e<0 it means that v is bellow v_ref. then apply positive acceleration to make v increase.
Most likely, this is what you do when driving (most of the time).
15/ Hence, following the strategy, we can apply negative terms in the original sequence when v is above v_ref and use the positive ones otherwise.
16/ But this raises the question: if v is below v_ref, how do we know that applying enough positive terms in the sequence will make v reach or surpass v_ref eventually?
17/ This is ensured since each series (with positive or negative elements only) is divergent. Applying a controller based only on the sequence's positive (or negative) elements makes the state diverge.
18/ Hence, we can apply the following controller, where we have a separate index "k" and "l" for positive and negative elements by separate, increased each time a controller applies one of the elements, ensuring no repeated elements. I use an algorithm here to simplify notation.
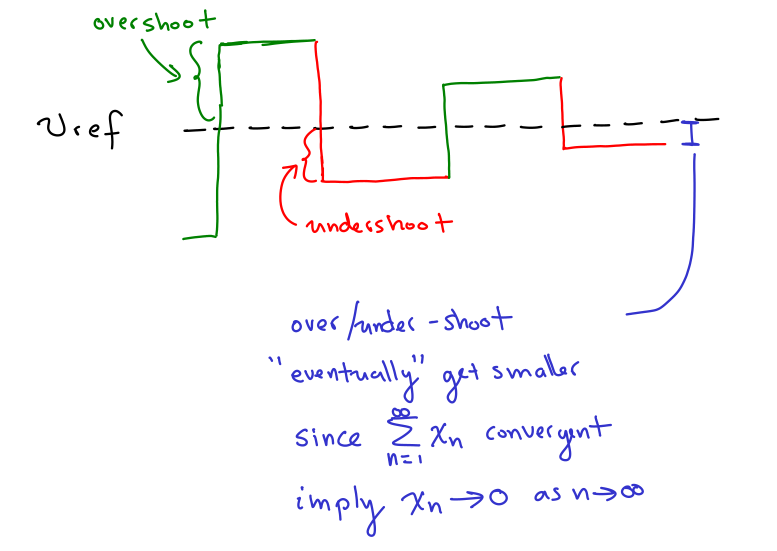
19/ This control strategy will induce the following behavior. If "v" starts below v_ref, you will add enough positive terms in the sequence until you surpass or reach exactly v_ref. Most likely, v will exceed v_ref; we call this an overshoot.
20/ Then, you apply negative elements of the sequence until v is below v_ref again. This is called an undershoot. Interestingly, since the original series is convergent, terms in the sequence eventually get smaller and smaller.
21/ This means that "overshoots" and "undershoots" get smaller and smaller. Hence, v will converge to v_ref, regardless of the value of v_ref! We can obtain the "rearrangement" by keeping track of the sequence elements applied at each step.
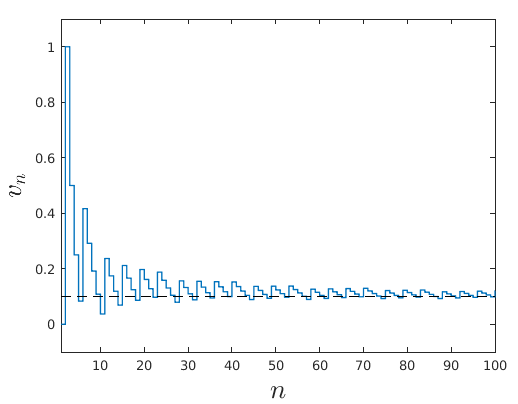
23/ For example, we can put a setpoint at v_ref=0.1. We start with a big overshoot since the first element of the sequence is 1. Then, three negative elements, namely -1/2, -1/4, -1/6, are applied to make v less than 0.1, and so on.
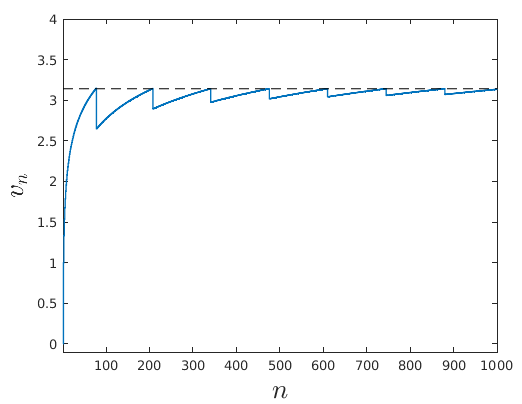
24/ Can we make the series add up to pi? Sure! At first, it takes a lot of steps for v to reach pi until we have a small overshoot. Since none of the negative elements have been used up to this point, we have a big undershoot from which we continue to add positive elements again.
25/ Note that the undershoots decrease in magnitude each time.
And that's it! You can rearrange a conditionally convergent series to converge to whatever you want by "controlling" the order of the elements in the partial sums using state feedback!
And that's it! You can rearrange a conditionally convergent series to converge to whatever you want by "controlling" the order of the elements in the partial sums using state feedback!