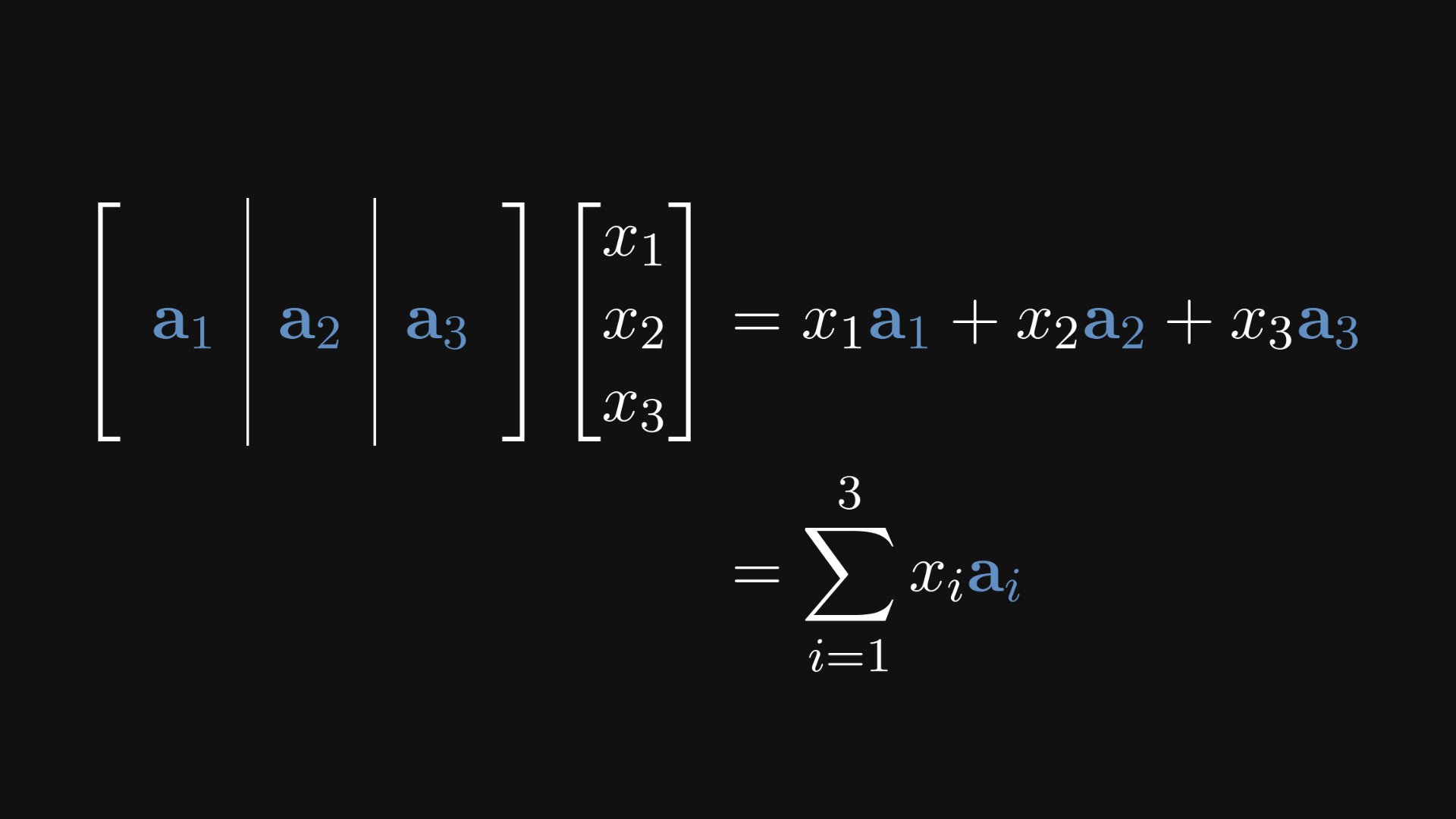Thread
Matrices + the Gram-Schmidt process = magic.
This magic is called the QR decomposition, and it's behind the famous eigenvalue-finding QR algorithm.
Here is how it works.
This magic is called the QR decomposition, and it's behind the famous eigenvalue-finding QR algorithm.
Here is how it works.
In essence, the QR decomposition factors an arbitrary matrix into the product of an orthogonal and an upper triangular matrix.
(We’ll illustrate everything with the 3 x 3 case, but everything works as is in general as well.)
(We’ll illustrate everything with the 3 x 3 case, but everything works as is in general as well.)
First, some notations. Every matrix can be thought of as a sequence of column vectors. Trust me, this simple observation is the foundation of many-many Eureka-moments in mathematics.
Why is this useful? Because this way, we can look at matrix multiplication as a linear combination of the columns.
Check out how matrix-vector multiplication looks from this angle. (You can easily work this out by hand if you don’t believe me.)
Check out how matrix-vector multiplication looks from this angle. (You can easily work this out by hand if you don’t believe me.)
In other words, a matrix times a vector equals a linear combination of the column vectors.
Similarly, the product of two matrices can be written in terms of linear combinations.
Similarly, the product of two matrices can be written in terms of linear combinations.
So, what’s the magic behind the QR decomposition? Simple: the vectorized version of the Gram-Schmidt process.
In a nutshell, the Gram-Schmidt process takes a linearly independent set of vectors and returns an orthonormal set that progressively generates the same subspaces.
In a nutshell, the Gram-Schmidt process takes a linearly independent set of vectors and returns an orthonormal set that progressively generates the same subspaces.
(If you are not familiar with the Gram-Schmidt process, check out my earlier thread, where I explain everything in detail.)
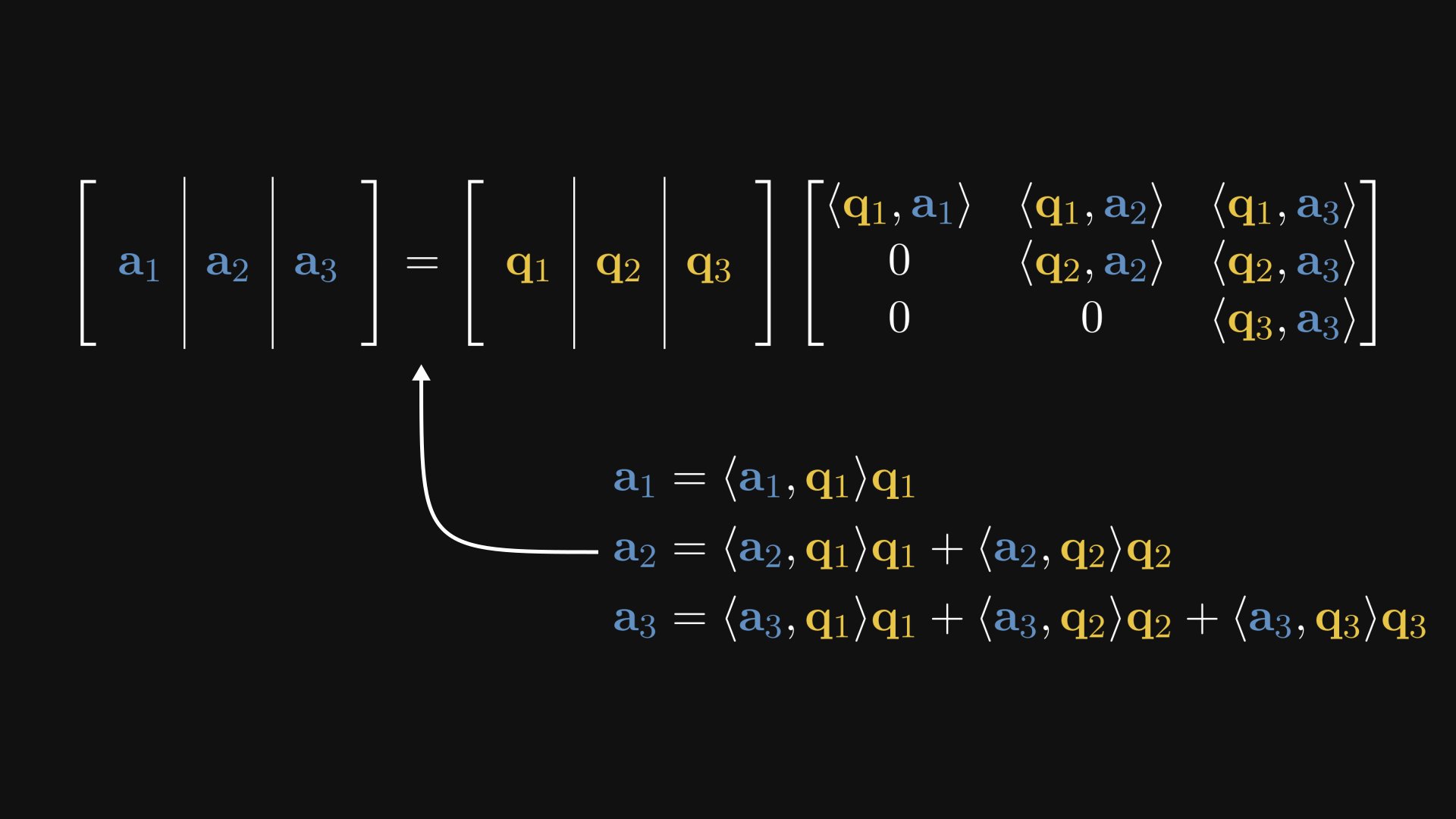
The output vectors of the Gram-Schmidt process (qᵢ) can be written as the linear combination of the input vectors (aᵢ).
In other words, using the column vector form of matrix multiplication, we obtain that in fact, A factors into the product of two matrices.
As you can see, one term is formed from the Gram-Schmidt process’ output vectors (qᵢ), while the other one is upper triangular.
However, the matrix of qᵢ-s is also special: as its columns are orthonormal, its inverse is its transpose. Such matrices are called orthogonal.
However, the matrix of qᵢ-s is also special: as its columns are orthonormal, its inverse is its transpose. Such matrices are called orthogonal.
Thus, any matrix can be written as the product of an orthogonal and an upper triangular one, which is the famous QR decomposition.
When is this useful for us? For one, it is used to iteratively find the eigenvalues of matrices. This is called the QR algorithm, one of the top 10 algorithms of the 20th century.
www.computer.org/csdl/magazine/cs/2000/01/c1022/13rRUxBJhBm
www.computer.org/csdl/magazine/cs/2000/01/c1022/13rRUxBJhBm
This explanation is also a part of my Mathematics of Machine Learning book.
It's for engineers, scientists, and other curious minds. Explaining math like your teachers should have, but probably never did. Check out the early access!
www.tivadardanka.com/books/mathematics-of-machine-learning
It's for engineers, scientists, and other curious minds. Explaining math like your teachers should have, but probably never did. Check out the early access!
www.tivadardanka.com/books/mathematics-of-machine-learning
If you have enjoyed this thread, share it with your friends and follow me!
I regularly post deep-dive explainers about mathematics and machine learning such as this.
I regularly post deep-dive explainers about mathematics and machine learning such as this.
Mentions
There are no mentions of this content so far.