Thread
Programmers need to use many number bases:
👉 decimal (the “normal” base);
👉 binary (10011001);
👉 hexadecimal (e.g., F8F8F2).
But you don't need advanced maths for them to make sense.
Read this. 👇
You'll wish you had done it sooner. 🚀
👉 decimal (the “normal” base);
👉 binary (10011001);
👉 hexadecimal (e.g., F8F8F2).
But you don't need advanced maths for them to make sense.
Read this. 👇
You'll wish you had done it sooner. 🚀
This whole thread was inspired by a course on @brilliantorg, a platform that teaches from first principles.
They break down concepts into interactive, bite-sized lessons (like the dots above).
But now, I want to show you how to work with number bases in a very intuitive way!
They break down concepts into interactive, bite-sized lessons (like the dots above).
But now, I want to show you how to work with number bases in a very intuitive way!
Honestly, just because 2 is a small number. 🤪
Let us start, then!
A “number base” is a specification about how to REPRESENT numbers.
The numbers, themselves, are always the same.
Right?
Let us start, then!
A “number base” is a specification about how to REPRESENT numbers.
The numbers, themselves, are always the same.
Right?
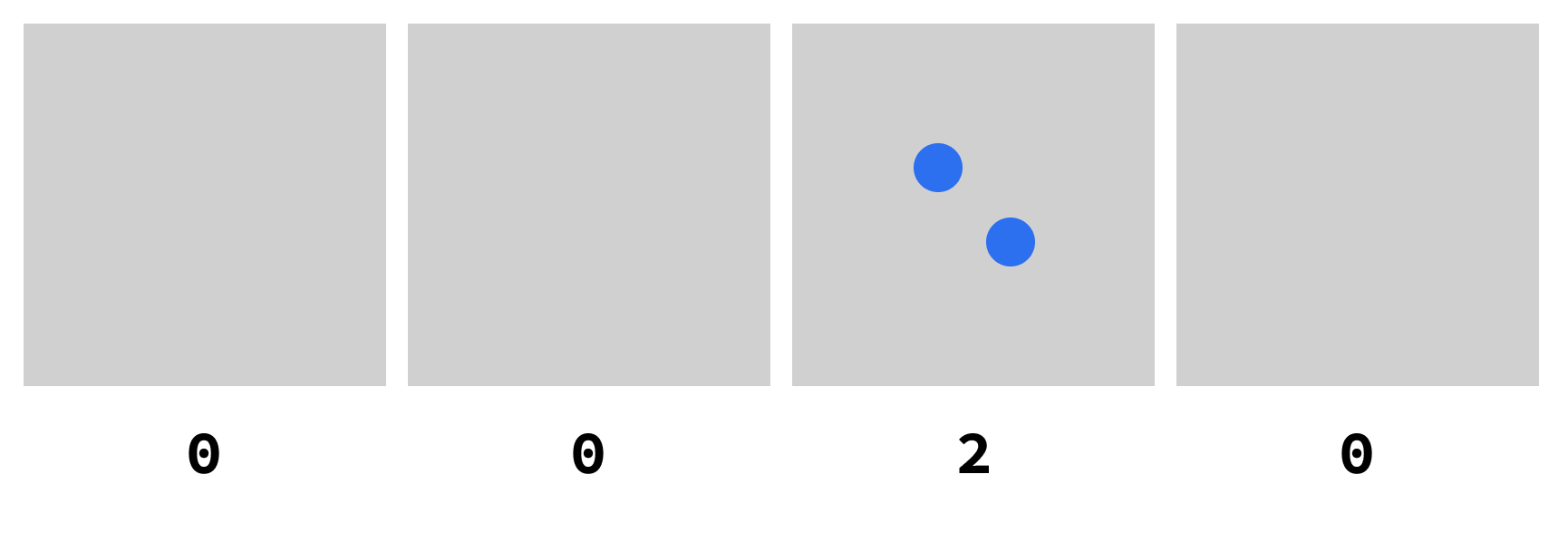
In the picture below, the left box has more dots than any other box, right?
You call that number “three” in English.
You call it “três” in Portuguese.
You call it “3” in the decimal base.
You call it “11” in the binary base.
But it is always the SAME number.
Agree?
You call that number “three” in English.
You call it “três” in Portuguese.
You call it “3” in the decimal base.
You call it “11” in the binary base.
But it is always the SAME number.
Agree?
So, a number base is just a mathematical language to give a name to a number.
And I am going to show you the rules.
For example, why is 138 written as
👉 10001010 in binary;
👉 212 in octal; and
👉 8A in hexadecimal?
(If you don't believe me, believe Python 🐍. 👇)
And I am going to show you the rules.
For example, why is 138 written as
👉 10001010 in binary;
👉 212 in octal; and
👉 8A in hexadecimal?
(If you don't believe me, believe Python 🐍. 👇)
Like I said, let us start with binary.
When you pick a number base, you pick a number.
You call that number the “base” of that number base.
For example, in binary, the base is 2.
In hexadecimal, the base is 16.
But what is that base for?
When you pick a number base, you pick a number.
You call that number the “base” of that number base.
For example, in binary, the base is 2.
In hexadecimal, the base is 16.
But what is that base for?
The base tells you how many symbols you can use to represent numbers in your number base language.
It's like the alphabet.
For example, the English alphabet has 26 symbols: ABC…XYZ.
The binary “alphabet” has 2: 01.
What now?
It's like the alphabet.
For example, the English alphabet has 26 symbols: ABC…XYZ.
The binary “alphabet” has 2: 01.
What now?
If the alphabet has the symbols 0 and 1, we can use those symbols to give names to numbers.
For example, “one hundred and thirty eight” is 10001010.
And “four” is 100.
But we're getting ahead of ourselves!
Let us start from the beginning:
For example, “one hundred and thirty eight” is 10001010.
And “four” is 100.
But we're getting ahead of ourselves!
Let us start from the beginning:
We could start by agreeing that “zero” is 0 in binary.
And might as well say that “one” is 1 in binary.
Now what?!
I used up all the symbols, so does that mean I can't represent more numbers?
And might as well say that “one” is 1 in binary.
Now what?!
I used up all the symbols, so does that mean I can't represent more numbers?
Of course that's NOT what that means!
We represent more numbers by combining 0s and 1s.
Again, “one hundred and thirty eight” could be 10001010 and “four” could be 100.
So, how to determine these longer representations?
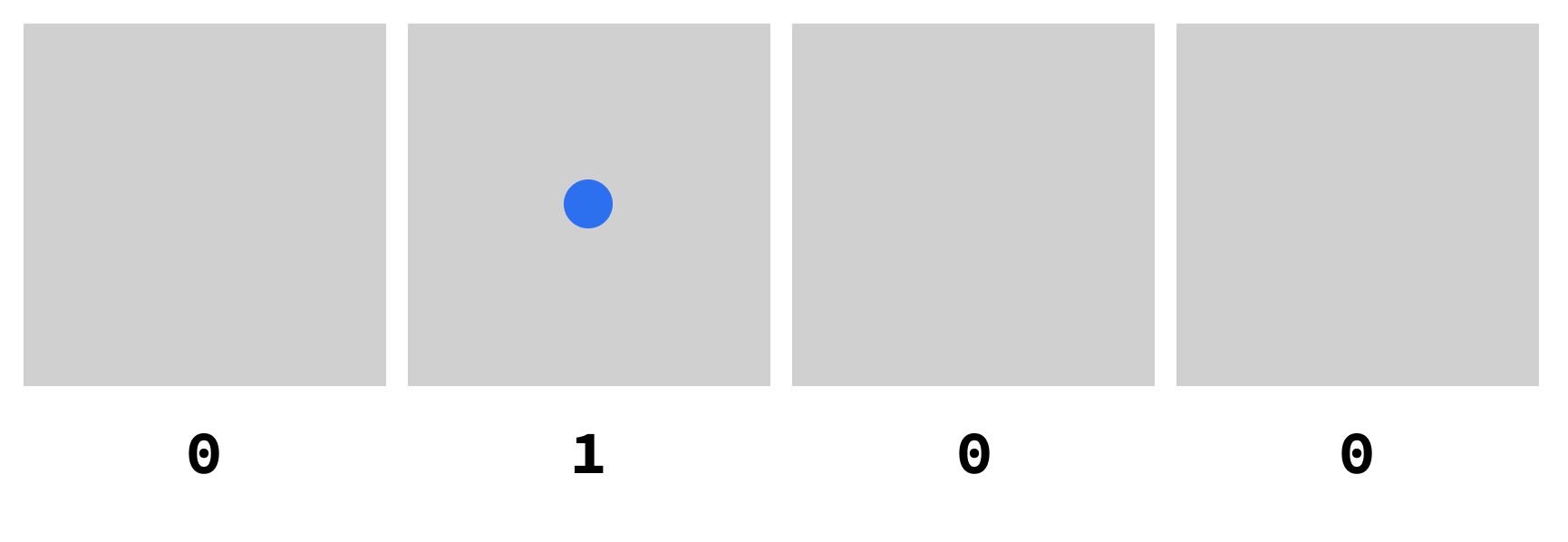
Let me show you how to do it for “four”:
We represent more numbers by combining 0s and 1s.
Again, “one hundred and thirty eight” could be 10001010 and “four” could be 100.
So, how to determine these longer representations?
Let me show you how to do it for “four”:
I took “four” dots and dropped them in the rightmost box below. 👇
Now, this is binary, so I need to play a game with the red dots.
Every time I find a group of 2 dots in the same box, I need to get rid of one and move the other to the left.
Let us see how that plays out:
Now, this is binary, so I need to play a game with the red dots.
Every time I find a group of 2 dots in the same box, I need to get rid of one and move the other to the left.
Let us see how that plays out:
I'll pick 2 dots from the rightmost box.
Next, I'll get rid of one and move the other to the left. 👇👈
Now, the rightmost box still has 2 dots.
So I'll get rid of one again and move the other to the left. 👇👉
Are we done, now?
Next, I'll get rid of one and move the other to the left. 👇👈
Now, the rightmost box still has 2 dots.
So I'll get rid of one again and move the other to the left. 👇👉
Are we done, now?
Nope, not really…
Now, I have 2 dots in the second rightmost box.
So, what do I do?
We get rid of one of the dots and move the other one to the left.
This is what we end up with, and we can stop now because there are no more groups of 2 dots in the same box.
Now, I have 2 dots in the second rightmost box.
So, what do I do?
We get rid of one of the dots and move the other one to the left.
This is what we end up with, and we can stop now because there are no more groups of 2 dots in the same box.
When we are done, we look at each box and use the symbol for the number of dots in each box.
The boxes with “zero” dots get a 0 and the boxes with “one” dot get a 1.
So, reading out the boxes and dots from the image above, what did the “four” dots become?
The boxes with “zero” dots get a 0 and the boxes with “one” dot get a 1.
So, reading out the boxes and dots from the image above, what did the “four” dots become?
The “four” dots became 00100 in binary.
But we get rid of the 0s on the left because they don't add anything…
So, how do we do this for any other base?
Instead of doing groups of 2 dots, we do groups with the size of the base!
In hexadecimal, we would do groups of…?
But we get rid of the 0s on the left because they don't add anything…
So, how do we do this for any other base?
Instead of doing groups of 2 dots, we do groups with the size of the base!
In hexadecimal, we would do groups of…?
16 dots!
We get rid of 15 dots and then move 1 dot to the left.
That's essentially the idea.
Keep bursting the dots until each box has a number of dots below the base number.
Let us do a crazy example. What is “thirty one” in base 30?
We get rid of 15 dots and then move 1 dot to the left.
That's essentially the idea.
Keep bursting the dots until each box has a number of dots below the base number.
Let us do a crazy example. What is “thirty one” in base 30?
Here are “thirty one” dots in a box.
We do a big group of 30 dots, get rid of 29, and move one to the left.
We are done, and we see that “thirty one” is represented by “11” in base 30.
We do a big group of 30 dots, get rid of 29, and move one to the left.
We are done, and we see that “thirty one” is represented by “11” in base 30.
As I said, this was inspired by a @brilliantorg course on Number Bases.
I'm quite impressed with what I learned by starting a course on a subject I thought I already knew! 😮
Click here to start a 30-day free trial + 20% off an annual subscription:
brilliant.org/mathspp
I'm quite impressed with what I learned by starting a course on a subject I thought I already knew! 😮
Click here to start a 30-day free trial + 20% off an annual subscription:
brilliant.org/mathspp