Thread
1/
Get a cup of coffee.
In this thread, we'll analyze the "Devil's Card Game".
This is a super useful thought exercise. It can teach us several key concepts in economics, probability, betting, hedging, investor/market psychology, etc.
Get a cup of coffee.
In this thread, we'll analyze the "Devil's Card Game".
This is a super useful thought exercise. It can teach us several key concepts in economics, probability, betting, hedging, investor/market psychology, etc.
2/
So, what's the Devil's Card Game?
Here's a description. Please take a moment to read through it -- as it forms the basis for the rest of this thread.
(h/t Professor Henk Tijms, @Hendrikc44)
So, what's the Devil's Card Game?
Here's a description. Please take a moment to read through it -- as it forms the basis for the rest of this thread.
(h/t Professor Henk Tijms, @Hendrikc44)
3/
So, we get to draw as many cards as we like -- up to 11 cards, one after another.
At each turn, we hope to double our money by drawing "double" cards.
But there's 1 "devil" card in the mix. If we draw it, more than 99.95% of our money ((2047/2048)'th of it) is gone. Poof!
So, we get to draw as many cards as we like -- up to 11 cards, one after another.
At each turn, we hope to double our money by drawing "double" cards.
But there's 1 "devil" card in the mix. If we draw it, more than 99.95% of our money ((2047/2048)'th of it) is gone. Poof!
4/
This is an exaggerated version of what happens in the stock market.
Most years, the market gives us a decent return.
But from time to time, a big crash occurs.
So, thinking through this card game can hopefully teach us a thing or two about investing in stocks.
This is an exaggerated version of what happens in the stock market.
Most years, the market gives us a decent return.
But from time to time, a big crash occurs.
So, thinking through this card game can hopefully teach us a thing or two about investing in stocks.
5/
In the Devil's Card Game, the ONLY thing under our control is when we walk away.
Our hope is: we'll get to double our $1M a few times, and then walk away safely before the "devil" appears.
Much like we hope to sell our stocks and walk away before the market crashes.
In the Devil's Card Game, the ONLY thing under our control is when we walk away.
Our hope is: we'll get to double our $1M a few times, and then walk away safely before the "devil" appears.
Much like we hope to sell our stocks and walk away before the market crashes.
6/
In the beginning, there are 11 cards on deck: 10 "double" cards and 1 "devil" card.
So, the chances of drawing a "double" are 10/11 = ~90.9%. Those are pretty good odds.
But as we draw more and more doubles, the odds of the next card being a double go down.
In the beginning, there are 11 cards on deck: 10 "double" cards and 1 "devil" card.
So, the chances of drawing a "double" are 10/11 = ~90.9%. Those are pretty good odds.
But as we draw more and more doubles, the odds of the next card being a double go down.
7/
For example, suppose we draw 6 doubles.
Now, there are 5 remaining cards on deck: 4 "doubles" and 1 "devil".
The probability of drawing a "double" now is only 4/5 = 80%.
Still pretty good odds, but not as high as when we started the game.
For example, suppose we draw 6 doubles.
Now, there are 5 remaining cards on deck: 4 "doubles" and 1 "devil".
The probability of drawing a "double" now is only 4/5 = 80%.
Still pretty good odds, but not as high as when we started the game.
8/
More than the *odds*, the real problem is the terrible *consequence* of drawing the "devil" -- ie, losing more than 99.95% of our money.
When we have events like this -- low *odds*, but terrible *consequences* -- we have to be very careful while deciding how to bet on them.
More than the *odds*, the real problem is the terrible *consequence* of drawing the "devil" -- ie, losing more than 99.95% of our money.
When we have events like this -- low *odds*, but terrible *consequences* -- we have to be very careful while deciding how to bet on them.
9/
One thing is clear:
If we ever draw the "devil", we know for sure that all *remaining* cards on deck are doubles -- as there's only 1 "devil".
So, *after* drawing the "devil", we should NOT walk away. We should stay for the full 11 draws, which will leave us with $500K.
One thing is clear:
If we ever draw the "devil", we know for sure that all *remaining* cards on deck are doubles -- as there's only 1 "devil".
So, *after* drawing the "devil", we should NOT walk away. We should stay for the full 11 draws, which will leave us with $500K.
10/
So, that's our worst case: we walk away with $500K.
What's the best case? That's if we draw 10 straight doubles. Then, we'll take home $1M * (2^10) = $1.024B.
(After 10 straight doubles, we know for sure that the last remaining card is the "devil". So, we won't draw it.)
So, that's our worst case: we walk away with $500K.
What's the best case? That's if we draw 10 straight doubles. Then, we'll take home $1M * (2^10) = $1.024B.
(After 10 straight doubles, we know for sure that the last remaining card is the "devil". So, we won't draw it.)
11/
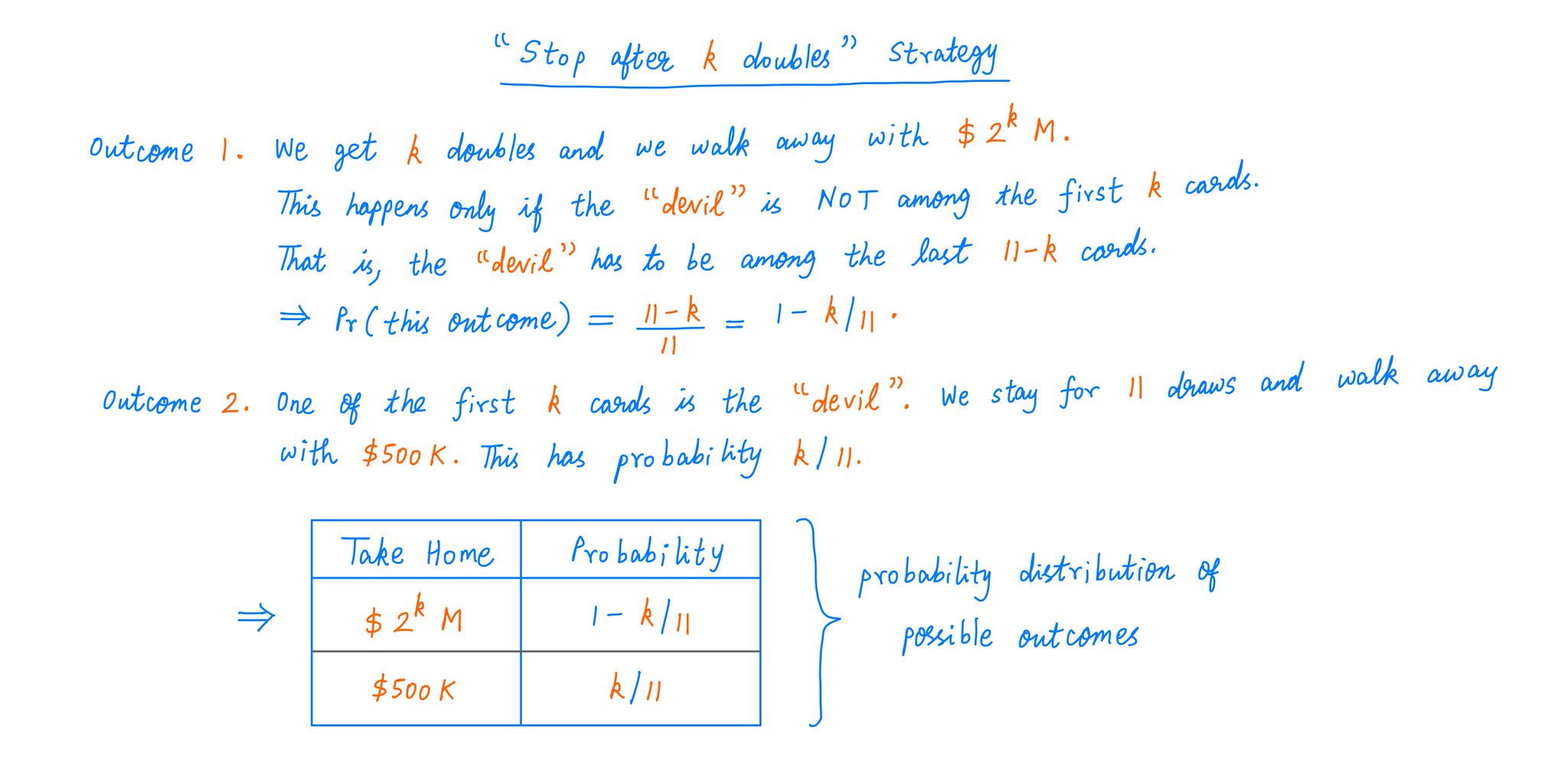
But we may not want to stick around that long. Why tempt the "devil"?
So, what if our strategy is to stop after drawing "k" doubles?
That is, we draw "k" cards. If they're all doubles, we walk away. If one of them is the "devil", we stay for 11 draws and take home $500K.
But we may not want to stick around that long. Why tempt the "devil"?
So, what if our strategy is to stop after drawing "k" doubles?
That is, we draw "k" cards. If they're all doubles, we walk away. If one of them is the "devil", we stay for 11 draws and take home $500K.
13/
So, what should our cut-off "k" be?
How many doubles before we take our money and walk away?
Each of us will have a different answer to this question -- depending on our risk tolerance, "utility function", etc.
Below, I'll walk you through some of these concepts.
So, what should our cut-off "k" be?
How many doubles before we take our money and walk away?
Each of us will have a different answer to this question -- depending on our risk tolerance, "utility function", etc.
Below, I'll walk you through some of these concepts.
14/
"Expectation Maximization" is one standard approach economists use to bet on such situations.
For each "walk away k", we have 2 possible outcomes. We find the *expected value* of these outcomes, and choose whichever "k" has the highest expected value.
Like so:
"Expectation Maximization" is one standard approach economists use to bet on such situations.
For each "walk away k", we have 2 possible outcomes. We find the *expected value* of these outcomes, and choose whichever "k" has the highest expected value.
Like so:
15/
So, IF our strategy is Expectation Maximization, we'll stay in the game almost all the way to the end.
But this strategy is very "bi-polar".
Sure, it gives us a ~9% chance of ending up a billionaire.
But there's a ~91% chance of losing $500K of our initial $1M!
So, IF our strategy is Expectation Maximization, we'll stay in the game almost all the way to the end.
But this strategy is very "bi-polar".
Sure, it gives us a ~9% chance of ending up a billionaire.
But there's a ~91% chance of losing $500K of our initial $1M!
16/
For example, after 9 doubles, we'll have $512M.
Why risk losing almost all of that on the 10'th draw -- which is essentially a "double or nothing" type bet?
Sure, if we win, we'll have $1.024B.
But what can we do with $1.024B that we can't with $512M?
For example, after 9 doubles, we'll have $512M.
Why risk losing almost all of that on the 10'th draw -- which is essentially a "double or nothing" type bet?
Sure, if we win, we'll have $1.024B.
But what can we do with $1.024B that we can't with $512M?
17/
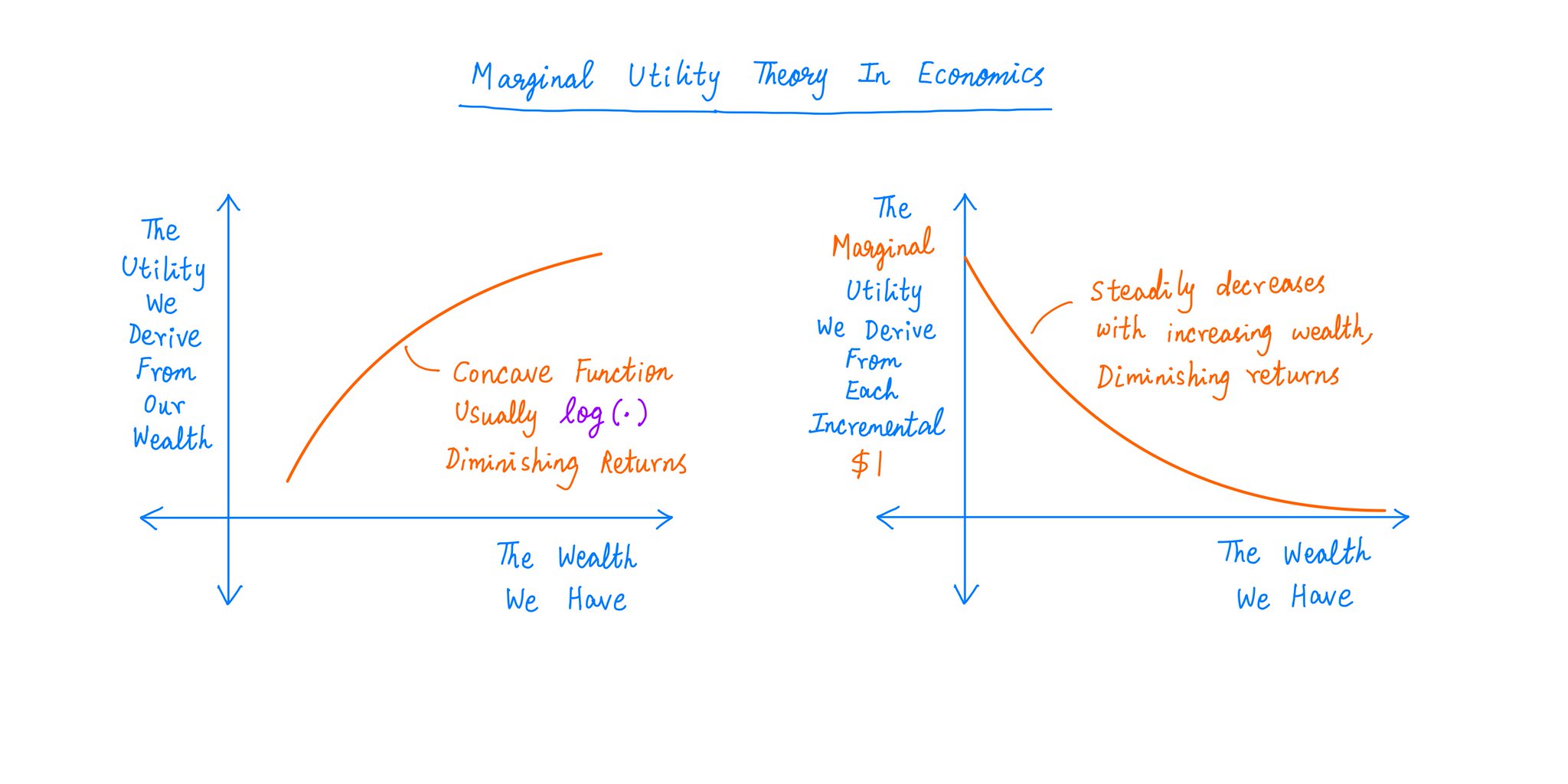
This is the crux of Marginal Utility Theory.
The key idea: Each dollar we have gives us some benefit. Some "utility".
But the MORE money we have, the LESS benefit we derive from each *additional* $1.
This is the crux of Marginal Utility Theory.
The key idea: Each dollar we have gives us some benefit. Some "utility".
But the MORE money we have, the LESS benefit we derive from each *additional* $1.
18/
For example, if you or I suddenly get a $1M windfall, it may be life changing.
But if Elon Musk or Jeff Bezos were to get the *same* $1M windfall, it would hardly make a difference to them.
To you or me, the *marginal utility* of $1M is HIGH.
To Elon or Jeff, it's LOW.
For example, if you or I suddenly get a $1M windfall, it may be life changing.
But if Elon Musk or Jeff Bezos were to get the *same* $1M windfall, it would hardly make a difference to them.
To you or me, the *marginal utility* of $1M is HIGH.
To Elon or Jeff, it's LOW.
19/
So, if $4M or $8M is a *significant* sum to us, the utility we'd LOSE by drawing the "devil" (and going back to $500K) may be much higher than any utility we might gain from scoring a few more doubles.
As Buffett wrote in his 2018 Bershire letter:
So, if $4M or $8M is a *significant* sum to us, the utility we'd LOSE by drawing the "devil" (and going back to $500K) may be much higher than any utility we might gain from scoring a few more doubles.
As Buffett wrote in his 2018 Bershire letter:
20/
So, for people like us playing the Devil's Card Game, Expected *Utility* Maximization may be a much better strategy than Expectation Maximization.
For example, if we're worth $2M, and we use $1M of it to play this game, our optimal strategy may be to stop after 6 doubles:
So, for people like us playing the Devil's Card Game, Expected *Utility* Maximization may be a much better strategy than Expectation Maximization.
For example, if we're worth $2M, and we use $1M of it to play this game, our optimal strategy may be to stop after 6 doubles:
21/
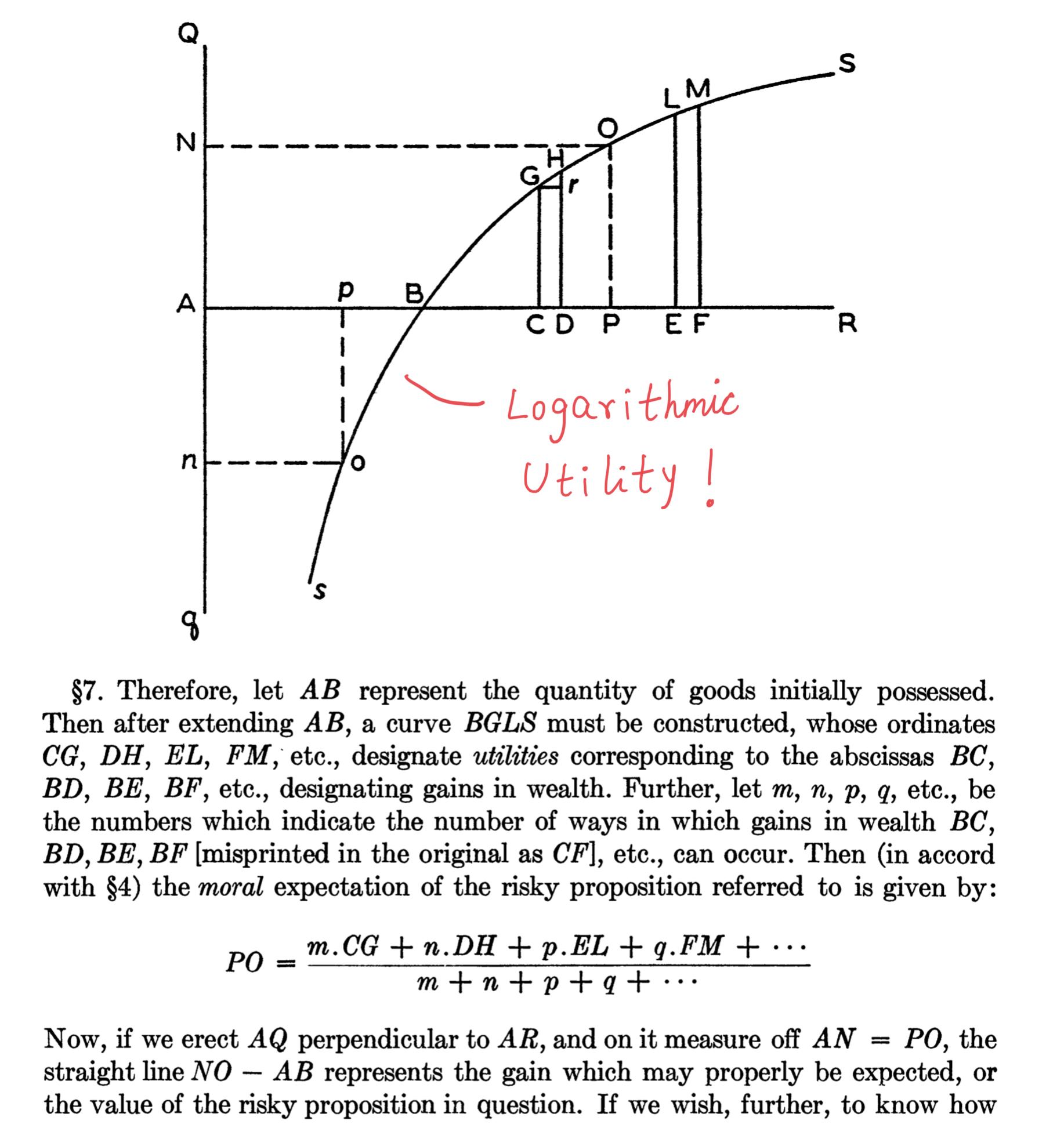
It was the great mathematician Daniel Bernoulli who worked out this "utility theory" -- way back in 1738!
Bernoulli figured out pretty much all the concepts above: concavity, logarithmic utility, Expected Utility Maximization, etc.
From his paper (econ.ucsb.edu/~tedb/Courses/GraduateTheoryUCSB/Bernoulli.pdf):
It was the great mathematician Daniel Bernoulli who worked out this "utility theory" -- way back in 1738!
Bernoulli figured out pretty much all the concepts above: concavity, logarithmic utility, Expected Utility Maximization, etc.
From his paper (econ.ucsb.edu/~tedb/Courses/GraduateTheoryUCSB/Bernoulli.pdf):
22/
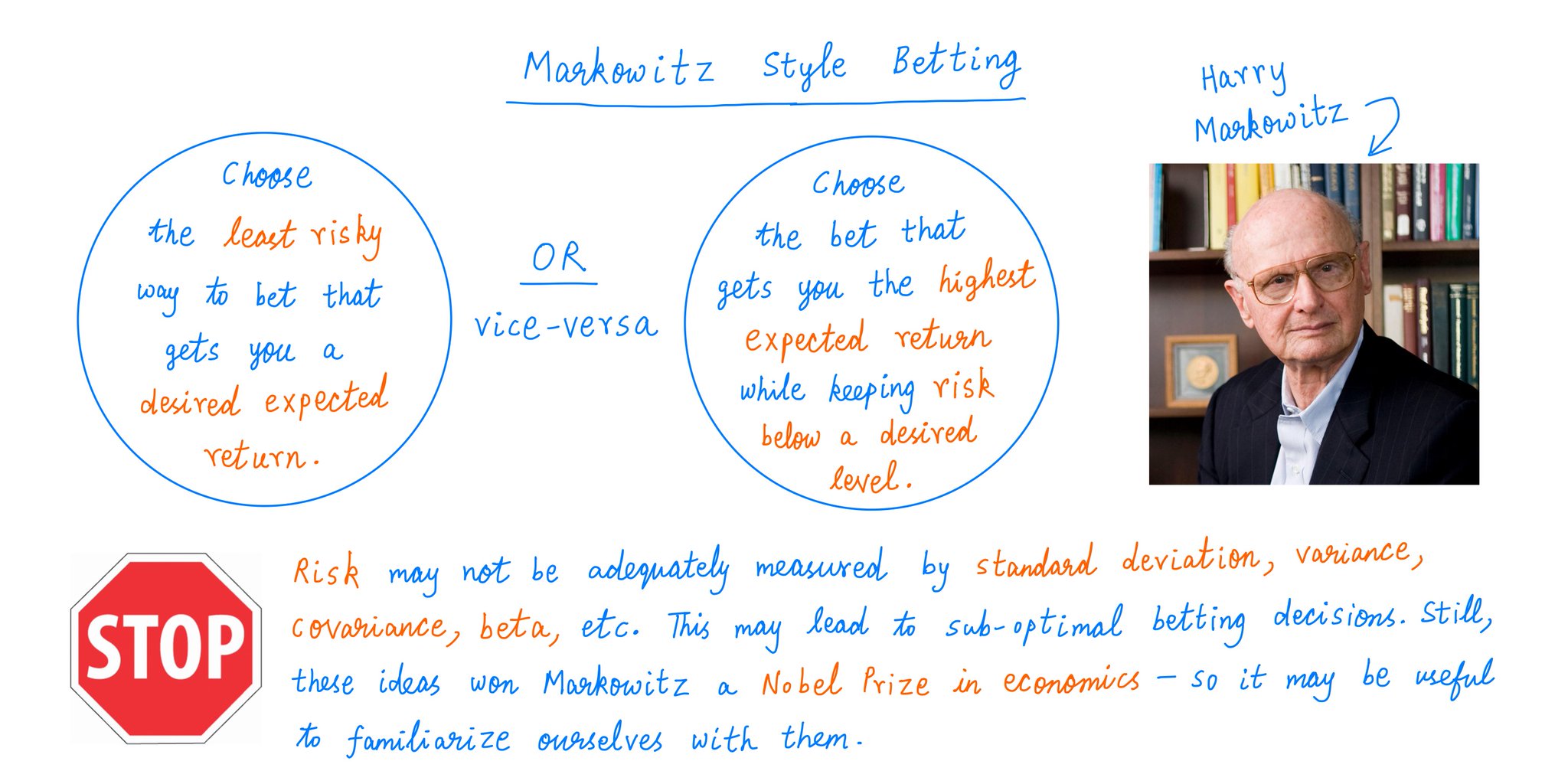
The great economist Harry Markowitz devised yet another betting strategy.
First, we pick an outcome -- the *lowest* amount of money we'd be happy to walk away with. Suppose this is $3M.
Now, we find the *least risky* way to walk away with an *expected* $3M.
Like so:
The great economist Harry Markowitz devised yet another betting strategy.
First, we pick an outcome -- the *lowest* amount of money we'd be happy to walk away with. Suppose this is $3M.
Now, we find the *least risky* way to walk away with an *expected* $3M.
Like so:
23/
One potential problem with Markowitz-style betting is how we measure risk.
For example, people like Buffett have often spoken out against traditional ways of measuring risk (eg, via beta). Short term volatility may not be equal to long term risk, etc.
One potential problem with Markowitz-style betting is how we measure risk.
For example, people like Buffett have often spoken out against traditional ways of measuring risk (eg, via beta). Short term volatility may not be equal to long term risk, etc.
24/
Kelly Style Betting is still another way to think about optimal strategies for such games.
This applies when we can *control* our bet sizes.
For example, instead of betting ALL our money at each draw, what if we could decide *how much* to bet at each turn?
Like so:
Kelly Style Betting is still another way to think about optimal strategies for such games.
This applies when we can *control* our bet sizes.
For example, instead of betting ALL our money at each draw, what if we could decide *how much* to bet at each turn?
Like so:
25/
The key elements of Kelly Style Betting are:
a) We bet only a *fraction* of our bankroll at each draw, and
b) We decide this fraction based on the *odds* of various possible outcomes.
For more:
The key elements of Kelly Style Betting are:
a) We bet only a *fraction* of our bankroll at each draw, and
b) We decide this fraction based on the *odds* of various possible outcomes.
For more:
26/
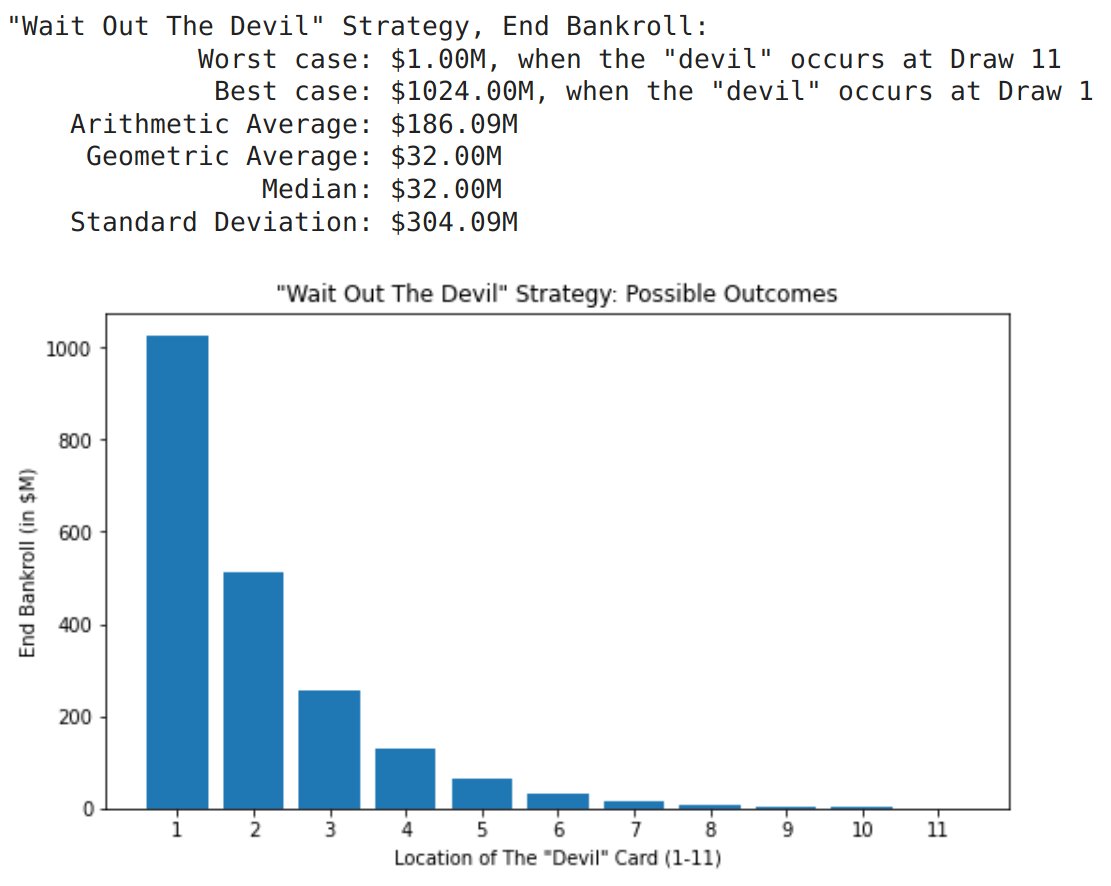
One way to play the game with adjustable bets is to simply "wait out" the devil.
That is, bet $0 at each draw until the devil appears, and then go ALL IN once the danger has passed.
In the worst case, the devil appears right at the end. Even so, we'll take home $1M.
One way to play the game with adjustable bets is to simply "wait out" the devil.
That is, bet $0 at each draw until the devil appears, and then go ALL IN once the danger has passed.
In the worst case, the devil appears right at the end. Even so, we'll take home $1M.
27/
So, there's a VERY wide spread of outcomes if our strategy is to "wait out the devil".
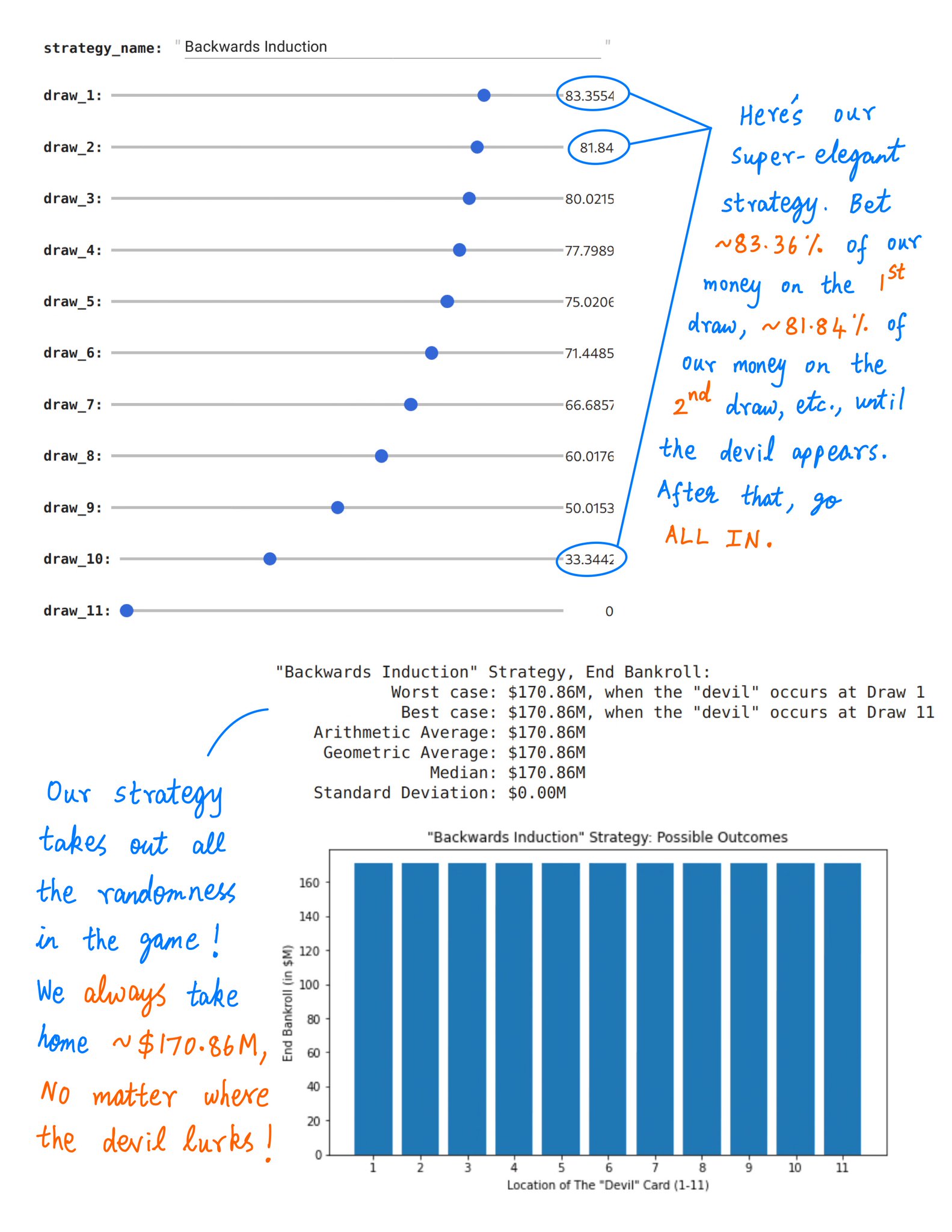
But there's a *different* way to bet -- called Backwards Induction.
It's super-elegant!
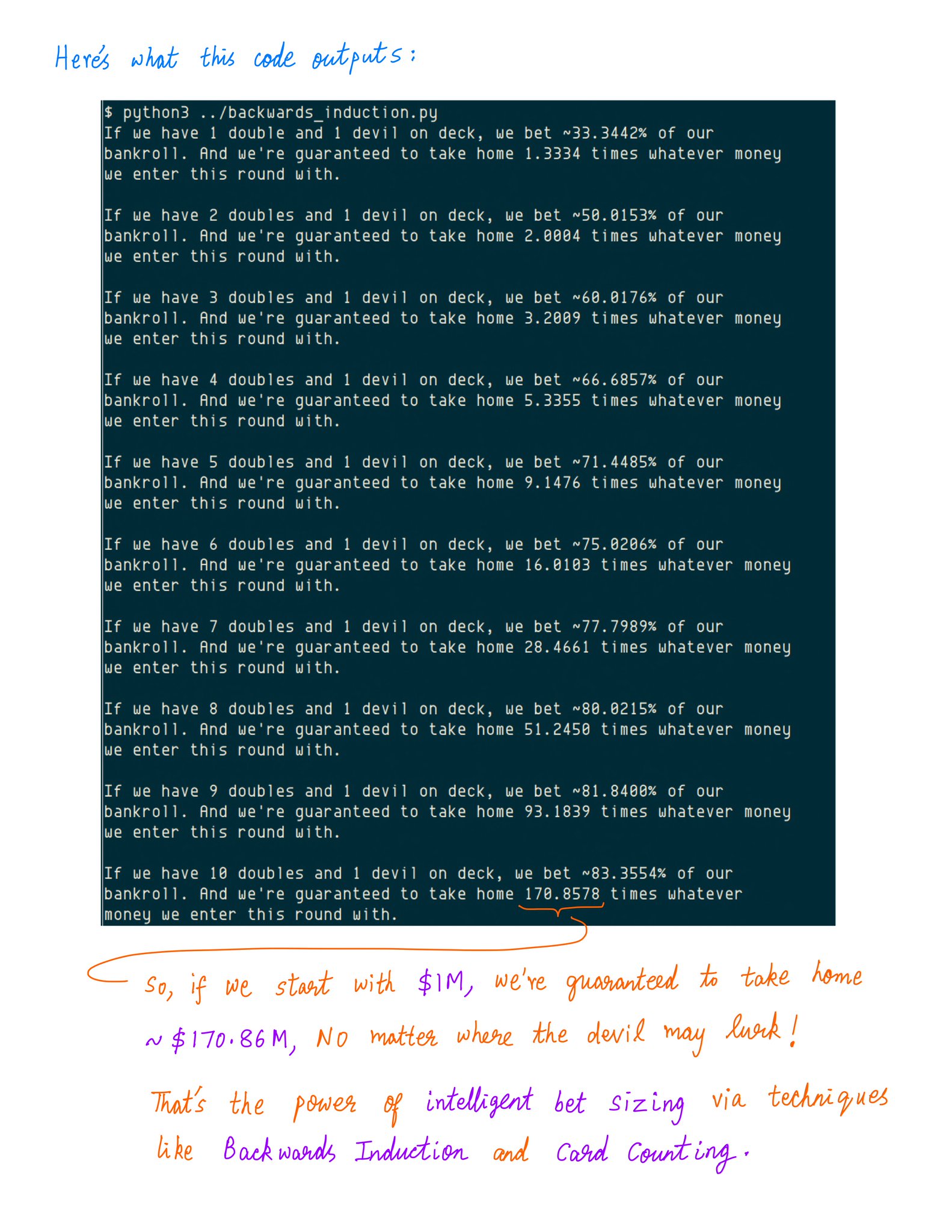
It *guarantees* that we'll take home ~$170.86M -- NO matter where the devil may lurk.
So, there's a VERY wide spread of outcomes if our strategy is to "wait out the devil".
But there's a *different* way to bet -- called Backwards Induction.
It's super-elegant!
It *guarantees* that we'll take home ~$170.86M -- NO matter where the devil may lurk.
28/
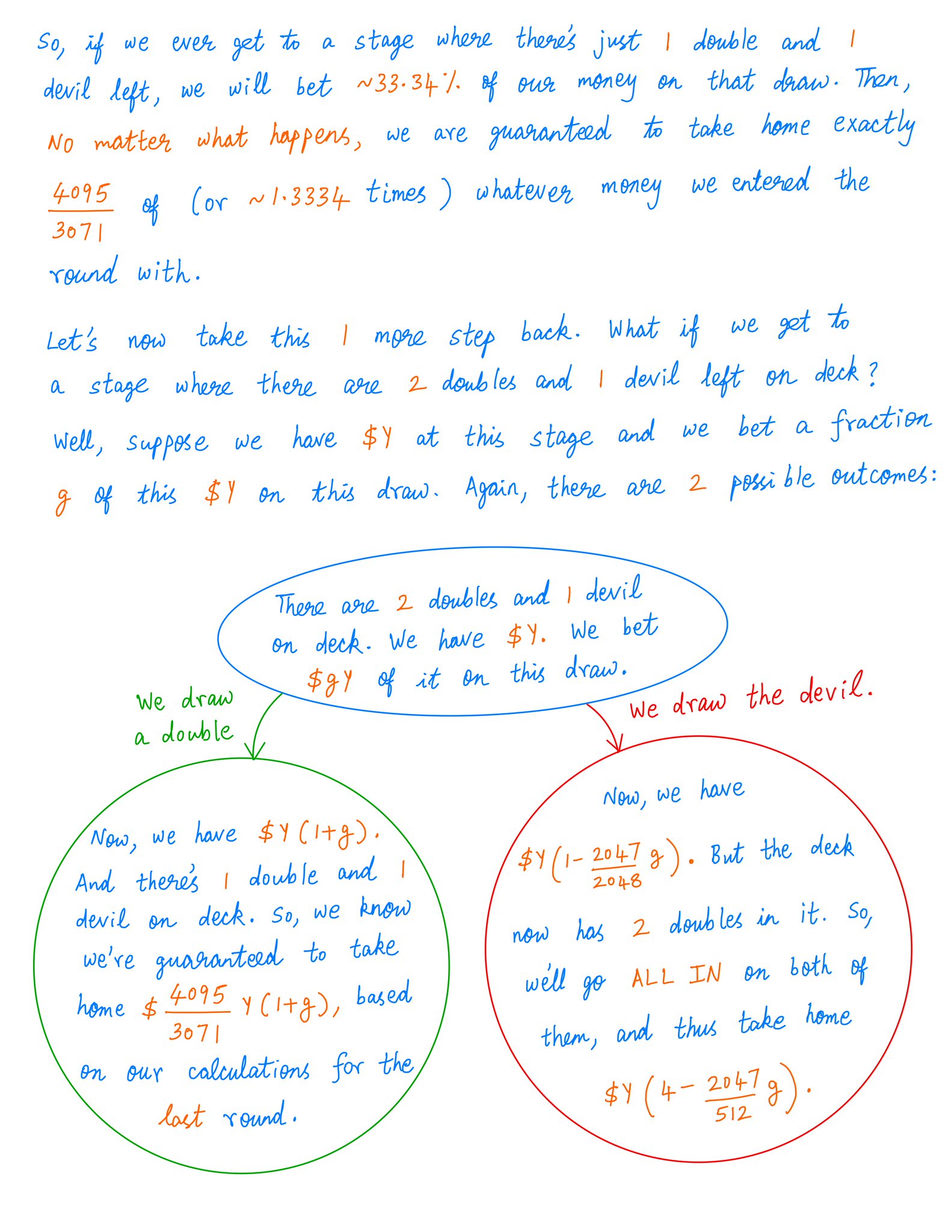
The key idea behind Backwards Induction is to start at the *last* round of the game.
Once we know our strategy for the *last* round, we work out our strategy for the *last but one* round.
And so on -- all the way back to the *first* round.
Like so:
The key idea behind Backwards Induction is to start at the *last* round of the game.
Once we know our strategy for the *last* round, we work out our strategy for the *last but one* round.
And so on -- all the way back to the *first* round.
Like so:
29/
Thus, bet sizing can have a HUGE impact.
Here we have a game where going ALL IN on 11 draws is *guaranteed* to LOSE us $500K.
BUT, with intelligent bet sizing, we turned this LOSER into a WINNER that *guarantees* us a ~$170M profit on a $1M investment.
Thus, bet sizing can have a HUGE impact.
Here we have a game where going ALL IN on 11 draws is *guaranteed* to LOSE us $500K.
BUT, with intelligent bet sizing, we turned this LOSER into a WINNER that *guarantees* us a ~$170M profit on a $1M investment.
30/
This is also what Card Counting is all about.
We track which cards have been drawn and which cards are still on deck.
This lets us calculate the odds of various outcomes.
Based on these odds, we apply Kelly, Backwards Induction, etc., to size our bets and profit!
This is also what Card Counting is all about.
We track which cards have been drawn and which cards are still on deck.
This lets us calculate the odds of various outcomes.
Based on these odds, we apply Kelly, Backwards Induction, etc., to size our bets and profit!
31/
If you want to learn more about Card Counting or Kelly Style Betting, I recommend the books and papers written by @EdwardOThorp.
His short book, Beat The Dealer, is a great way to dive into these topics:
www.amazon.com/Beat-Dealer-Winning-Strategy-Twenty-One/dp/0394703103/
If you want to learn more about Card Counting or Kelly Style Betting, I recommend the books and papers written by @EdwardOThorp.
His short book, Beat The Dealer, is a great way to dive into these topics:
www.amazon.com/Beat-Dealer-Winning-Strategy-Twenty-One/dp/0394703103/
32/
So, we've covered 4 betting strategies:
(i) Expectation Maximization,
(ii) Expected Utility Maximization,
(iii) Markowitz Style Betting, and
(iv) Kelly Style Betting (+ Backwards Induction, Card Counting).
All are useful to know before betting on a bunch of probabilities.
So, we've covered 4 betting strategies:
(i) Expectation Maximization,
(ii) Expected Utility Maximization,
(iii) Markowitz Style Betting, and
(iv) Kelly Style Betting (+ Backwards Induction, Card Counting).
All are useful to know before betting on a bunch of probabilities.
33/
In addition to these *quantitative* topics, the Devil's Card Game can also teach us *psychology*.
For example, many people fall prey to the House Money Effect.
They change how they play based on whether the initial $1M is "their own hard earned money" or "house money".
In addition to these *quantitative* topics, the Devil's Card Game can also teach us *psychology*.
For example, many people fall prey to the House Money Effect.
They change how they play based on whether the initial $1M is "their own hard earned money" or "house money".
34/
But this is not very rational.
As soon as the $1M is available to *take out*, it makes NO difference where it *came from*.
But if it's "house money", many of us are MORE likely to risk it on such "double or halve" type bets.
But this is not very rational.
As soon as the $1M is available to *take out*, it makes NO difference where it *came from*.
But if it's "house money", many of us are MORE likely to risk it on such "double or halve" type bets.
35/
Closely related to the House Money Effect is the Sunk Cost Fallacy.
When we've sunk money and effort into a bet, we find it difficult to cut our losses short and exit the position -- even if it's clear we made a mistake going in.
"The stock does not know our cost basis!"
Closely related to the House Money Effect is the Sunk Cost Fallacy.
When we've sunk money and effort into a bet, we find it difficult to cut our losses short and exit the position -- even if it's clear we made a mistake going in.
"The stock does not know our cost basis!"
36/
Prospect Theory and Loss Aversion (psychological effects popularized by the great behavioral scientists Daniel Kahneman and Amos Tversky) also play a role here.
Put simply: We feel the pain of a $1 loss more acutely than the pleasure of a $1 gain.
Prospect Theory and Loss Aversion (psychological effects popularized by the great behavioral scientists Daniel Kahneman and Amos Tversky) also play a role here.
Put simply: We feel the pain of a $1 loss more acutely than the pleasure of a $1 gain.
37/
For more on these psychological effects, I recommend reading Kahneman and Tversky's book, "Thinking, Fast and Slow":
www.amazon.com/Thinking-Fast-Slow-Daniel-Kahneman/dp/0374533555/
For more on these psychological effects, I recommend reading Kahneman and Tversky's book, "Thinking, Fast and Slow":
www.amazon.com/Thinking-Fast-Slow-Daniel-Kahneman/dp/0374533555/
38/
I also very much like Charlie Munger's speech, The Psychology of Human Misjudgment.
In this speech, Munger masterfully goes through a checklist of 25 common psychological biases and pitfalls investors tend to suffer from:
(h/t @ShaneAParrish): fs.blog/great-talks/psychology-human-misjudgment/
I also very much like Charlie Munger's speech, The Psychology of Human Misjudgment.
In this speech, Munger masterfully goes through a checklist of 25 common psychological biases and pitfalls investors tend to suffer from:
(h/t @ShaneAParrish): fs.blog/great-talks/psychology-human-misjudgment/
39/
So, there you have it.
So many quantitative *and* psychological lessons -- all drawn from one card game.
Now you know why I find this game so fascinating!
For more, here's our recent Money Concepts episode about it (~1 hr, 19 min audio):
callin.com/link/MtgiNJMjWu
So, there you have it.
So many quantitative *and* psychological lessons -- all drawn from one card game.
Now you know why I find this game so fascinating!
For more, here's our recent Money Concepts episode about it (~1 hr, 19 min audio):
callin.com/link/MtgiNJMjWu
40/
If you're still with me, thank you very much!
I hope this thread introduced you to some useful concepts.
And I hope you had as much fun delving into them as I had researching the game!
/End
If you're still with me, thank you very much!
I hope this thread introduced you to some useful concepts.
And I hope you had as much fun delving into them as I had researching the game!
/End
Mentions
See All
Ben Hunt @EpsilonTheory
·
Apr 14, 2022
Excellent work!